Who

Carsten Wulff

Why

Example of a temperature sensor

How

One way to make a temperature sensor is to create a temperature dependent oscillator, and then measure the frequency of the oscillator. In Figure 0 we can see an overview.

A bandgap circuit is used to make a current that is proportional to absolute temperature ($I_{PTAT}$) and a voltage that is complementary to absolute temperature ($V_{CTAT}$). A relaxation oscillator converts the current and voltage into a frequency ($f_{OSC}$). A digital finite-state-machine and a counter converts the frequency to a digital value that is proportional to temperature.

_{Figure 0: System overview}

This temperature sensor was made to conform to the specification at The Project: Design a temperature sensor.

For more information on the oscillator, see Schematics.

To measure the frequency of the oscillator we need a frequency reference. One reference that is usually available in a MCU system is a 32768 Hz oscillator ($f_{32KI}$ in Figure 0). The reason for that specific frequency is to accurately be able to count to 1 second with a binary counter, and apparently to have a frequency for the crystal that is higher than 20 kHz, so we can’t hear it (according to https://youtu.be/_2By2ane2I4?si=8ltUNqAPL71zCQUW).

The principle of operation of the FSM and counter can be seen in Figure 1.

The FSM starts in a IDLE state where a counter is reset. Next the temperature dependent oscillator is started, and a number of oscillator pulses are counted. The FSM runs on LF_CLK and we use the count x LF_CLK to measure the oscillation frequency.

After one clock period the FSM powers down the oscillator. In the CAPTURE state the value of the counter is stored, and the FSM returns to idle.

_{Figure 1: Finite-State Machine to control temperature sensor}

A waveform of the sequence can be seen in Figure 2. When the signal start is asserted the FSM transitions to power up the oscillator (pwrupOsc=1), and we can notice the clkOsc counts the clock pulses of the oscillator. On the next lfClk the oscillator is shut down and the counter naturally stops. The value from the oscillator is stored in the cycles register.

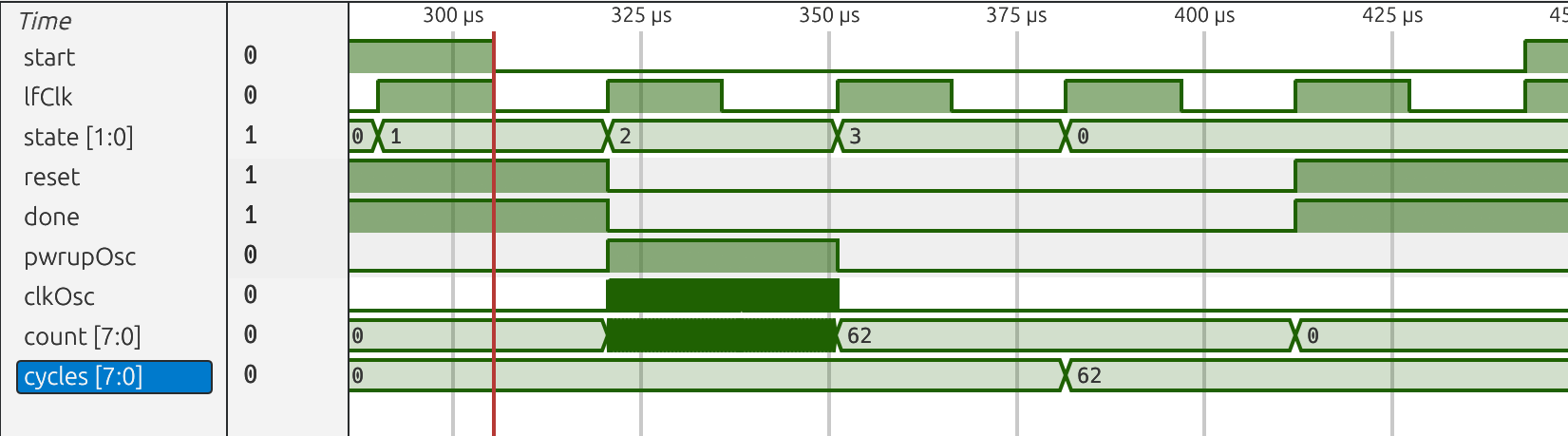
_{Figure 2: Waves from simulation of the oscillator}

In the testbench I store the cycles, and the testbench temperature to a file, and use tb.py to plot the transfer function.

I use a physical model of the oscillator (LELO_TEMP.py) to create a function to turn the frequency back to a temperature. It can be seen that the frequency has a non-zero second order derivative, and thus, the shape of the curve needs to be compensated for. See the python model for details.

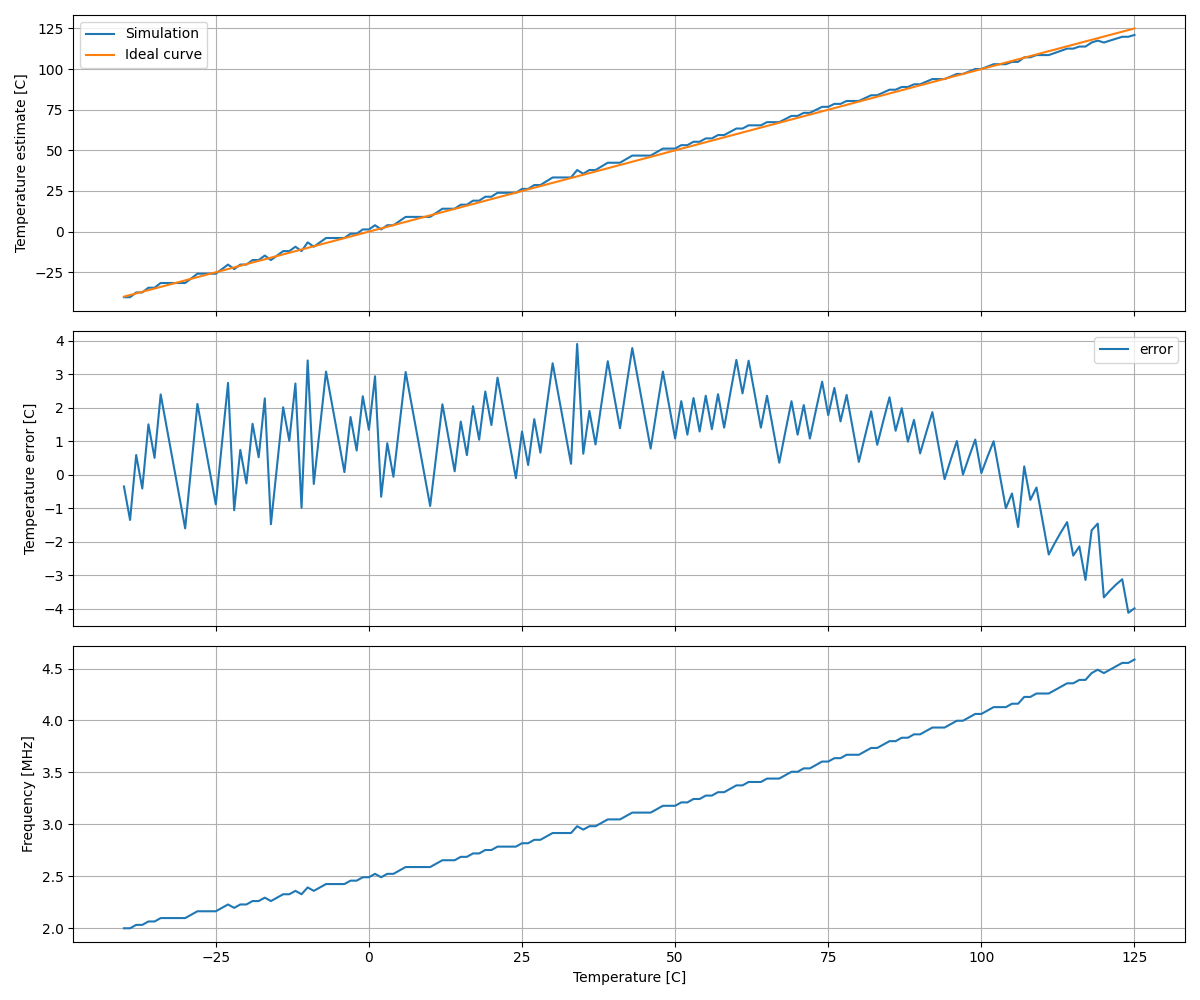
_{Figure 3: Simulation of the verilog model of the oscillator}

What

What	Cell/Name
Schematic	design/LELO_TEMP_SKY130A/LELO_TEMP.sch
Layout	design/LELO_TEMP_SKY130A/LELO_TEMP.mag
Verilog Model	design/LELO_TEMP_SKY130A/LELO_TEMP.v
Verilog Counter	rtl/tempCounter.v
Verilog Fsm	rtl/tempFsm.v
Verilog TB	sim/tb_lelo_temp/tb.v
Analog top TB	sim/LELO_TEMP/tran.spi

Signal interface

Signal	Direction	Domain	Description
VDD_1V8	Input	VDD_1V8	Main supply
PWRUP_1V8	Input	VDD_1V8	Power up the temperature dependent oscillator
OSC_TEMP_1V8	Output	VDD_1V8	Temperature dependent frequency
VSS	Input	Ground

Key parameters

Parameter	Min	Typ	Max	Unit
Technology		Skywater 130 nm
AVDD	1.7	1.8	1.9	V
Oscillation frequency	1.7	3.0	4.0	MHz
Temperature	-40	27	125	C

Simulation graphs

Typical temperature error of the sensor is low, but I’ve calibrated the second order correction for typical conditions.

Over mismatch and extreme test condition (ETC) the temperature error increase.

_{Figure 4: Typical simulation results of the oscillator}

_{Figure 5: Mismatch simulation of the oscillator}

_{Figure 6: Extreme test conditions (PVT) simulation of oscillator}