Slides
TFE4152 - Lecture 19
All radios started with Euler
\[e^{ix} = cos(x) + i sin(x)\]
\[e^{-ix} = cos(-x) - i sin(-x) = cos(x) - i sin(x)\]

\[e^{ix} = cos(x) + i sin(x)\]
\[e^{-ix} = cos(-x) - i sin(-x) = cos(x) - i sin(x)\]
\[cos(x) = e^{ix} - i sin(x)\]
\[-i sin(x) = e^{-ix} - cos(x)\]
\[cos(x) = e^{ix} + e^{-ix} - cos(x)\]
\[cos(x) = \frac{e^{ix} + e^{-ix}}{2}\]
\[cos(x) \times cos(y) = \frac{e^{ix} + e^{-ix}}{2} \times \frac{e^{iy}
+e^{-iy}}{2}\]
\[\rightarrow \frac{1}{4}\left[ e^{ix}e^{iy} + e^{-ix}e^{iy} + e^{ix}e^{-iy} + e^{-ix}e^{-iy}\right]\]
\[\rightarrow \frac{1}{4}\left[e^{i(x+y)} + e^{-i(x-y)} + e^{i(x-y)} + e^{-i (x + y)}\right]\]
\[\rightarrow \frac{1}{2}\left[\frac{e^{i(x+y)}+ e^{-i (x +y)}}{2} + \frac{e^{i(x-y)} + e^{-i (x-y)}}{2}\right]\]
\[\Rightarrow cos(x) \times cos(y) =\frac{1}{2}\left[cos(x+y) + cos(x-y)\right]\]
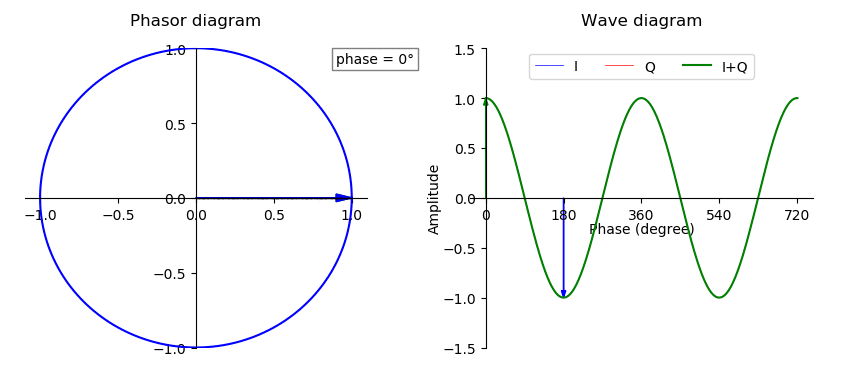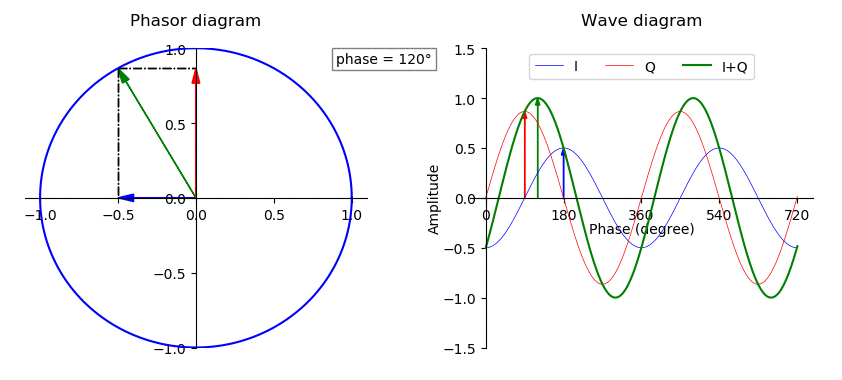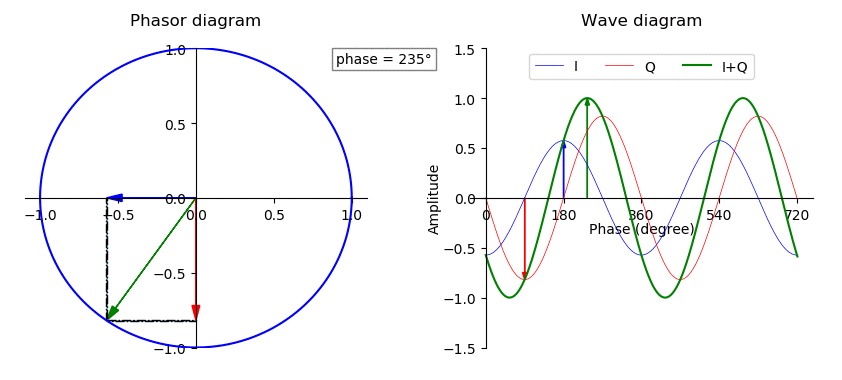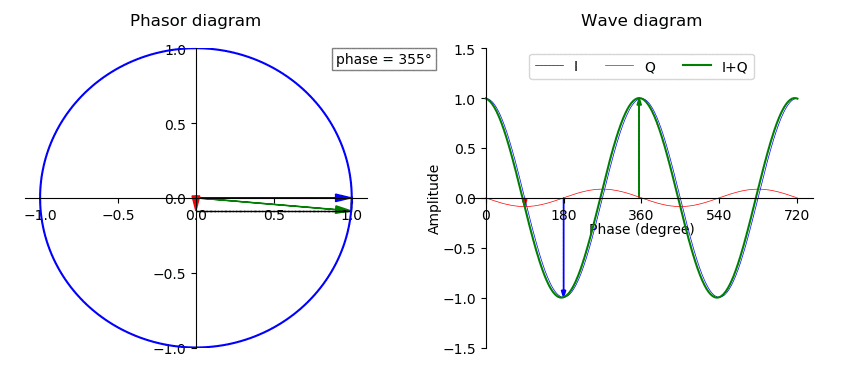
An ideal square wave is an infinite sum of odd harmonics
\[x(t) = \frac{4}{\pi}\sum_{k=1}^{\infty}\frac{sin(2\pi(2k - 1)ft)}{2k-1}\]

Complex Signal Processing is Not
Complex




