lectures/l19_radios

TFE4152 - Lecture 19

All radios started with Euler

Source

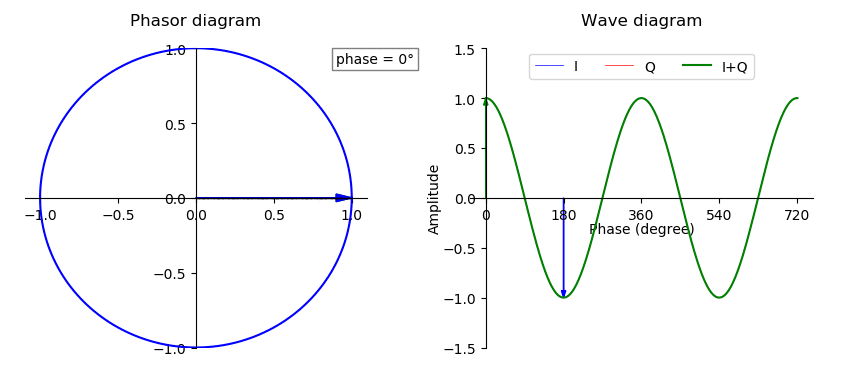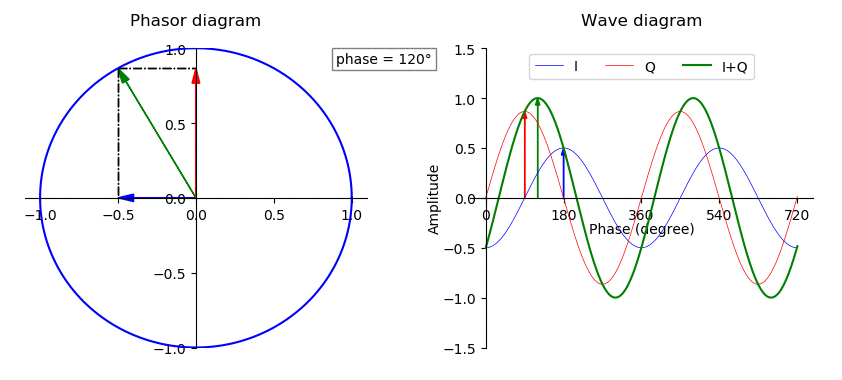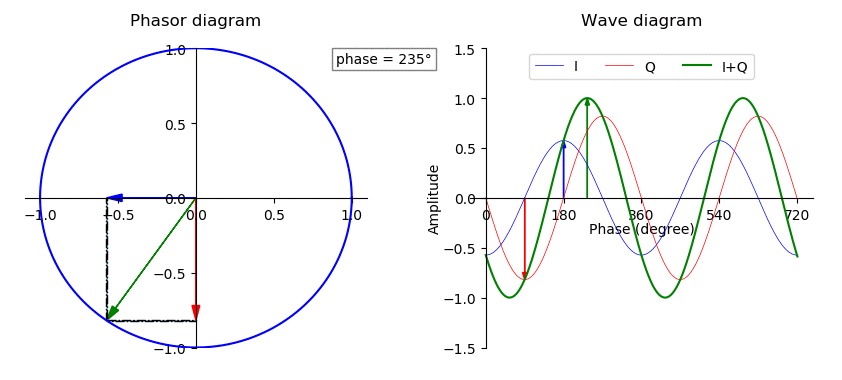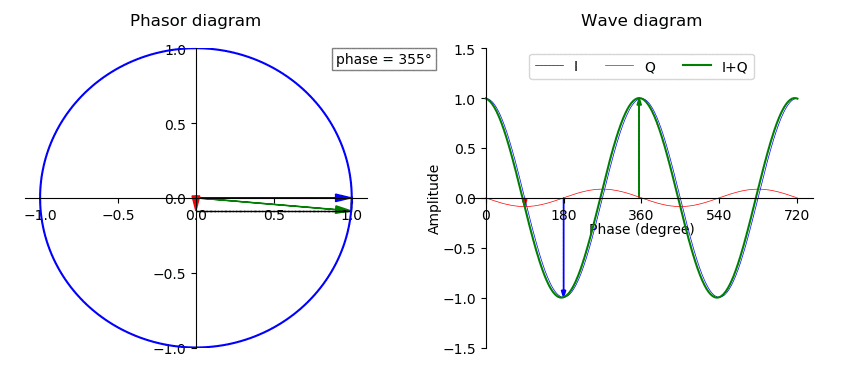
e^ix = cos(x) + isin(x)

e^−ix = cos(−x) − isin(−x) = cos(x) − isin(x)

e^ix = cos(x) + isin(x)

e^−ix = cos(−x) − isin(−x) = cos(x) − isin(x)

cos(x) = e^ix − isin(x)

 − isin(x) = e^−ix − cos(x)

cos(x) = e^ix + e^−ix − cos(x)

$$ cos(x) = \frac{e^{ix} + e^{-ix}}{2}$$

$$ cos(x) \times cos(y) = \frac{e^{ix} + e^{-ix}}{2} \times \frac{e^{iy} +e^{-iy}}{2} $$

$$ \rightarrow \frac{1}{4}\left[ e^{ix}e^{iy} + e^{-ix}e^{iy} + e^{ix}e^{-iy} + e^{-ix}e^{-iy}\right]$$

$$ \rightarrow \frac{1}{4}\left[e^{i(x+y)} + e^{-i(x-y)} + e^{i(x-y)} + e^{-i (x + y)}\right]$$

$$ \rightarrow \frac{1}{2}\left[\frac{e^{i(x+y)}+ e^{-i (x +y)}}{2} + \frac{e^{i(x-y)} + e^{-i (x-y)}}{2}\right]$$

$$\Rightarrow cos(x) \times cos(y) =\frac{1}{2}\left[cos(x+y) + cos(x-y)\right]$$

An ideal square wave is an infinite sum of odd harmonics

$$ x(t) = \frac{4}{\pi}\sum_{k=1}^{\infty}\frac{sin(2\pi(2k - 1)ft)}{2k-1} $$

Complex Signal Processing is Not Complex

Thanks!