Slides

TFE4152 - Lecture 14

Speed

Source

Week Book Monday Book Friday
34   Introduction, what are we going to do in this course. Why do you need it? WH 1 , WH 15 Manufacturing of integrated circuits
35 CJM 1.1 pn Junctions CJM 1.2 WH 1.3, 2.1-2.4 Mosfet transistors
36 CJM 1.2 WH 1.3, 2.1-2.4 Mosfet transistors CJM 1.3 - 1.6 Modeling and passive devices
37   Guest Lecture - Sony CJM 3.1, 3.5, 3.6 Current mirrors
38 CJM 3.2, 3.3,3.4 3.7 Amplifiers CJM, CJM 2 WH 1.5 SPICE simulation
39   Verilog   Verilog
40 WH 1.4 WH 2.5 CMOS Logic WH 3 Speed
41 WH 4 Q & A WH 5 Power/Wires
42 WH 6 Scaling Reliability and Variability WH 8 Gates
43 WH 9 Sequencing WH 10 Datapaths - Adders
44 WH 10 Datapaths - Multipliers, Counters WH 11 Memories
45 WH 12 Packaging WH 14 Test
46   Guest lecture - Nordic Semiconductor    
47 CJM Recap of CJM WH Recap of WH

dicex/sim/verilog/counter_sv video on youtube https://youtu.be/dbt1aQsu_3I

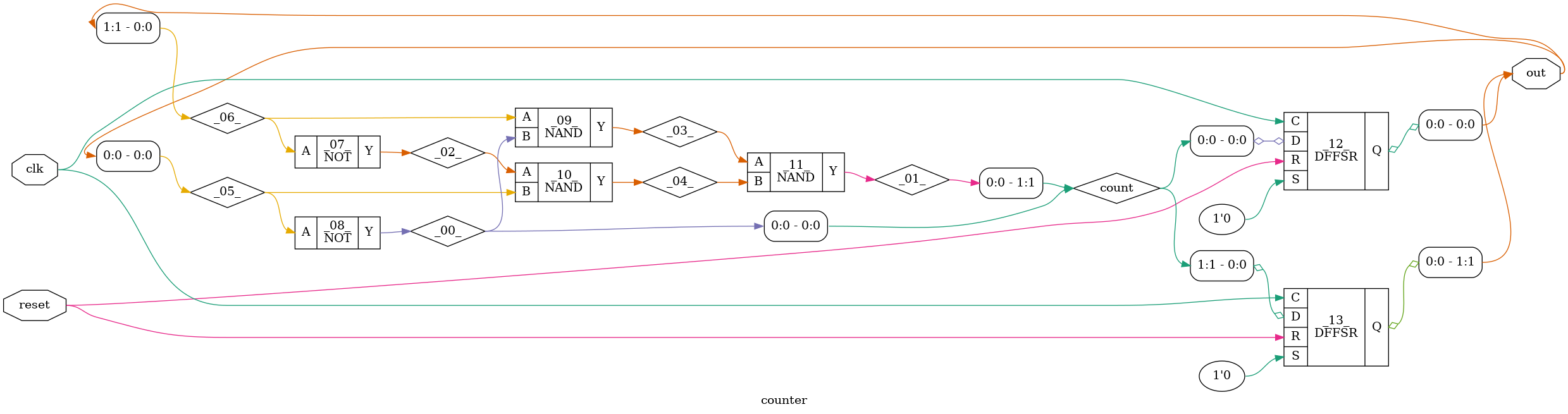
module counter(
               output logic [WIDTH-1:0] out,
               input logic              clk,
               input logic              reset
               );

   parameter WIDTH = 8;

   logic [WIDTH-1:0]                    count;
   always_comb begin
      count = out + 1;
   end

   always_ff @(posedge clk or posedge reset) begin
      if (reset)
        out <= 0;
      else
        out <= count;
   end

endmodule // counter

Speed

Why

Flip-flops and speed

dicex/lib/SUN_TR_GF130N.spi:

.SUBCKT DFRNQNX1_CV D CK RN Q QN AVDD AVSS
XA0 AVDD AVSS TAPCELLB_CV
XA1 CK RN CKN AVDD AVSS NDX1_CV
XA2 CKN CKB AVDD AVSS IVX1_CV
XA3 D CKN CKB A0 AVDD AVSS IVTRIX1_CV
XA4 A1 CKB CKN A0 AVDD AVSS IVTRIX1_CV
XA5 A0 A1 AVDD AVSS IVX1_CV
XA6 A1 CKB CKN QN AVDD AVSS IVTRIX1_CV
XA7 Q CKN CKB RN QN AVDD AVSS NDTRIX1_CV
XA8 QN Q AVDD AVSS IVX1_CV
.ENDS

Setup time: How long before clk does the data need to change

Hold time: How long after clk can the data change

Digital timing challenge: Estimate and analyze all delays over PVT

Timing analysis

Analyze arrival times of all nodes in a combinatorial circuit

\[arrival_j = max_{j \in fanin(i)}{arrival_j} + t_{pd_i} \Rightarrow a_j = max_{j \in fanin(i)}{a_j} + t_{pd_i}\] \[slack_i = required_i - arrival_j\]

Positive slack (over PVT1) \(\Rightarrow\) Timing is OK Negative slack (over PVT1) \(\Rightarrow\) Timing is not OK

Timing analysis tools

Commercial Cadence Tempus

Synopsys PrimeTime

Free OpenTimer

What is timing analysis

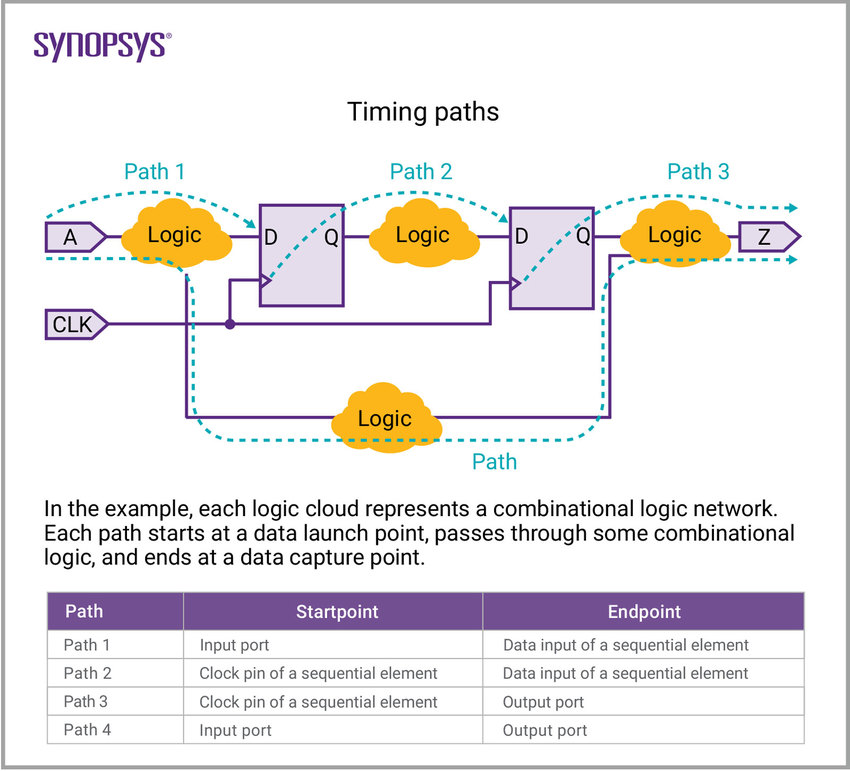
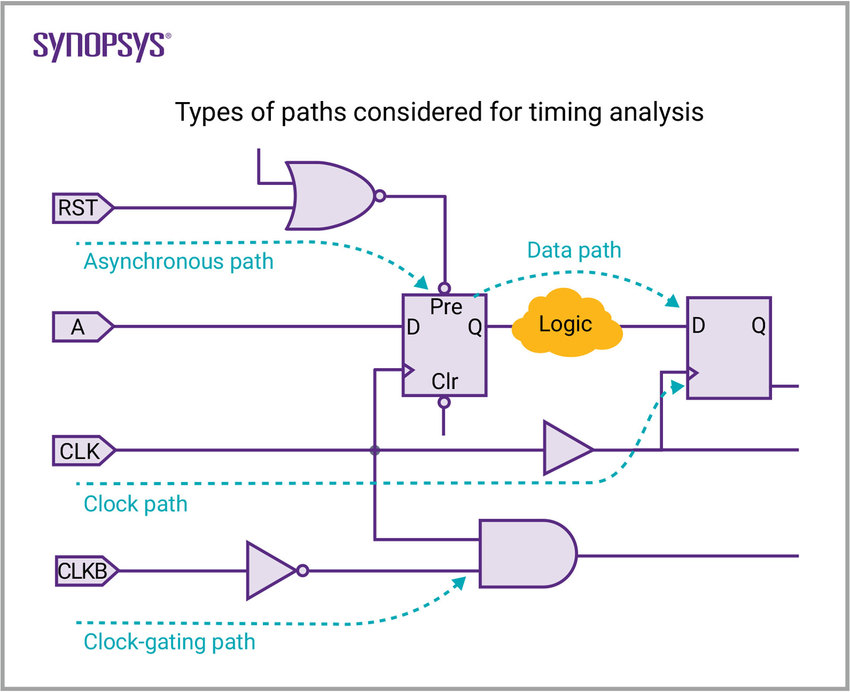
What do the tools need?

Input and output delay paths as a function of input transition time and capacitive load, setup and hold time.

osu018_stdcells.lib


cell (INVX1) {
  cell_footprint : inv;
area : 16;
  cell_leakage_power : 0.0221741;
  pin(A)  {
    direction : input;
    capacitance : 0.00932456;
    rise_capacitance : 0.00932196;
    fall_capacitance : 0.00932456;
  }
  pin(Y)  {
    direction : output;
    capacitance : 0;
    rise_capacitance : 0;
    fall_capacitance : 0;
    max_capacitance : 0.503808;
    function : "(!A)";
    timing() {
      related_pin : "A";
      timing_sense : negative_unate;
      cell_fall(delay_template_5x5) {
        index_1 ("0.005, 0.0125, 0.025, 0.075, 0.15");
        index_2 ("0.06, 0.18, 0.42, 0.6, 1.2");
        values ( \
          "0.030906, 0.037434, 0.038584, 0.039088, 0.030318", \
          "0.04464, 0.057551, 0.073142, 0.077841, 0.081003", \
          "0.064368, 0.091076, 0.11557, 0.126352, 0.144944", \
          "0.139135, 0.174422, 0.232659, 0.261317, 0.321043", \
          "0.249412, 0.28434, 0.357694, 0.406534, 0.51187");
      }
      

      fall_transition(delay_template_5x5) {
        index_1 ("0.005, 0.0125, 0.025, 0.075, 0.15");
        index_2 ("0.06, 0.18, 0.42, 0.6, 1.2");
        values ( \
          "0.032269, 0.0648, 0.087, 0.1032, 0.1476", \
          "0.036025, 0.0726, 0.1044, 0.1236, 0.183", \
          "0.06, 0.0882, 0.1314, 0.1554, 0.2286", \
          "0.1494, 0.1578, 0.2124, 0.2508, 0.3528", \
          "0.288, 0.2892, 0.3192, 0.3576, 0.492");
      }
      cell_rise(delay_template_5x5) {
        index_1 ("0.005, 0.0125, 0.025, 0.075, 0.15");
        index_2 ("0.06, 0.18, 0.42, 0.6, 1.2");
        values ( \
          "0.037639, 0.056898, 0.083401, 0.104927, 0.156652", \
          "0.05258, 0.083003, 0.119028, 0.141927, 0.207952", \
          "0.07402, 0.112622, 0.162437, 0.191122, 0.271755", \
          "0.15767, 0.201007, 0.284096, 0.331746, 0.452958", \
          "0.285016, 0.326868, 0.415086, 0.481337, 0.653064");
      }
      rise_transition(delay_template_5x5) {
        index_1 ("0.005, 0.0125, 0.025, 0.075, 0.15");
        index_2 ("0.06, 0.18, 0.42, 0.6, 1.2");
        values ( \
          "0.031447, 0.059488, 0.0846, 0.0918, 0.138", \
          "0.047167, 0.0786, 0.1044, 0.1224, 0.1734", \
          "0.072, 0.096, 0.1398, 0.1578, 0.222", \
          "0.1866, 0.1914, 0.2358, 0.2748, 0.3696", \
          "0.3648, 0.3648, 0.384, 0.4146, 0.5388");
      }
    }
    internal_power() {
      related_pin : "A";
      fall_power(energy_template_5x5) {
        index_1 ("0.005, 0.0125, 0.025, 0.075, 0.15");
        index_2 ("0.06, 0.18, 0.42, 0.6, 1.2");
        values ( \
          "0.009213, 0.004772, 0.00823, 0.018532, 0.054083", \
          "0.009047, 0.005677, 0.005713, 0.015244, 0.049453", \
          "0.008669, 0.006332, 0.002998, 0.01159, 0.04368", \
          "0.007879, 0.007243, 0.001451, 0.004701, 0.030385", \
          "0.007605, 0.007297, 0.003652, 0.000737, 0.020842");
      }
      rise_power(energy_template_5x5) {
        index_1 ("0.005, 0.0125, 0.025, 0.075, 0.15");
        index_2 ("0.06, 0.18, 0.42, 0.6, 1.2");
        values ( \
          "0.023555, 0.029044, 0.041387, 0.051684, 0.087278", \
          "0.023165, 0.028621, 0.039211, 0.048916, 0.083039", \
          "0.023574, 0.02752, 0.036904, 0.045723, 0.077971", \
          "0.024479, 0.025247, 0.032268, 0.039242, 0.066587", \
          "0.024942, 0.025187, 0.029612, 0.034835, 0.057524");
      }
    }
  }
}

Every gate must be simulated to provide behavior over input transition and load capacitance

All analog blocks must have associated liberty file to describe behavior and timing paths If you integrate analog into digital top flow

Gate Delay

Delay definitions

Parameter Name Description
t_pdr max rising propagation delay input to rising output cross 50 %
t_pdf max falling propagation delay input to falling output cross 50 %
t_pd propagation delay t_pdf = (t_pdr + t_pdf)/2
t_r rise time 20 % to 80 %

image ../ip/l14/delay_def.pdf removed

Delay definitions

| Parameter | Name| Description| | :– | :–| :–| | t_f | fall time | 80 % to 20 %| | t_cdr | min rising contamination delay | input to rising output cross 50 %| | t_cdf | min falling contamination delay | input to falling output cross 50 %| | t_cd | contamination delay | t_cd = (t_cdr + t_cdf)/2|

image ../ip/l14/delay_def.pdf removed

Delay estimation

How can we get a resonably accurate hand calculation model of delay?

\[C \approx 1 \text{ fF}/\mu\text{m}\] \[R \approx 1 \text{ k}\Omega\mu\text{m}\]

image ../ip/l14/rc_pmos.pdf removed> image ../ip/l14/rc_nmos.pdf removed

Inverter with inverter load

\(C \approx 1 \text{ fF}/\mu\text{m}\), \(R \approx 1 \text{ k}\Omega\mu\text{m}\)

\[t_{pd} = R \times 6C = 6RC\] \[t_{pd} = 6 \times 1 \times 10^{3} \times 1 \times 10^{-15} \text{ s}\] \[t_{pd} = 6 \times 10^{-12} = 6 \text{ ps}\]

image ../ip/l14/inv.pdf removed

It’s not a perfect model, but it’s good enough for hand calculation

Figure from Weste book

image ../ip/l14/rc_fit.pdf removed

Elmore Delay

\[t_{pd} \approx \sum_{\text{nodes}}{R_{\text{nodes}-to-source} C_i}\] \[= R_1C_1 + (R_1 + R_2)C_2 + ... + (R_1 + R_2 + ... + R_N) C_N\]

Good enough for hand calculation

image ../ip/l14/elmore.pdf removed

Delay of 3-input NAND

image ../ip/l14/nand3.pdf removed

image ../ip/l14/nand.pdf removed image ../ip/l14/nand_tr.pdf removed

image ../ip/l14/nand_pu.pdf removed

\[t_{pdr} = (9 + 5h)C\]

image ../ip/l14/nand_pd.pdf removed Use Elmore

\[t_{pdf} = 3C\frac{R}{3} + 3C\frac{2R}{3} + (9 + 5h)C\frac{3R}{3}\] \[= (12 + 5h)RC\]

Assume \(h = 1\), \(RC \approx 1 \text{ ps}\)

Contamination delay

\[t_{cdr} = (9 + 5h)C\frac{R}{3} = (3 + \frac{5}{3}h)RC\] \[t_{cdr} = 4\frac{2}{3} \text{ ps}\]

Propagation delay

\[t_{pdr} = (9 + 5h)RC = 14 \text{ ps}\] \[t_{pdf}= (12 + 5h)RC = 17 \text{ ps}\]

Delay components

Parasitic delay (p)

p = 9 or 12 RC

Independent of load capacitance

Effort delay (f)

f = 5h RC

Proportional to load capacitance

Let’s use process independent unit \(d = \frac{d_{real}}{\tau}\), \(\tau = 3 RC\)

Parasitic delay \(\Rightarrow p = 12 RC / 3 RC = 4\)

Effort delay \(\Rightarrow f = 5h RC / 3RC = \frac{5}{3} h\)

Delay \(\Rightarrow d = f + p = \frac{5}{3}h + 4\)

Logical effort (g) is the ratio of the input capacitance of a gate to the input capacitance of an inverter delivering the same output current

image ../ip/l14/logical_effort.pdf removed

Parasitic delay \(\Rightarrow p = 4\)

Logic effort \(\Rightarrow g = \frac{5}{3}\)

Electrical effort \(\Rightarrow h = 1\)

Effort \(\Rightarrow f = gh\)

Delay \(\Rightarrow d = f + p = gh + p = 5\frac{2}{3}\)

Real delay \(\Rightarrow d = 5\frac{2}{3} \times 3 \text{ ps} = 17 \text{ ps}\)

Modern IC timing analysis requires computers with advanced programs2

Best number of stages

Which has shortest delay?

\[H = C_{cout}/C_{in} = 64\] \[G = \prod{g_i} = \prod{1} = 1\] \[B = 1\] \[F = GBH = 64\]

One stage \(f = 64 \Rightarrow D = 64 + 1 = 65\)

Three stage with \(f=4\) \(D_F = 12, p = 3 \Rightarrow D = 12 + 3 = 15\)

For close to optimal delay, use \(f = 4\) (Used to be \(f=e\))

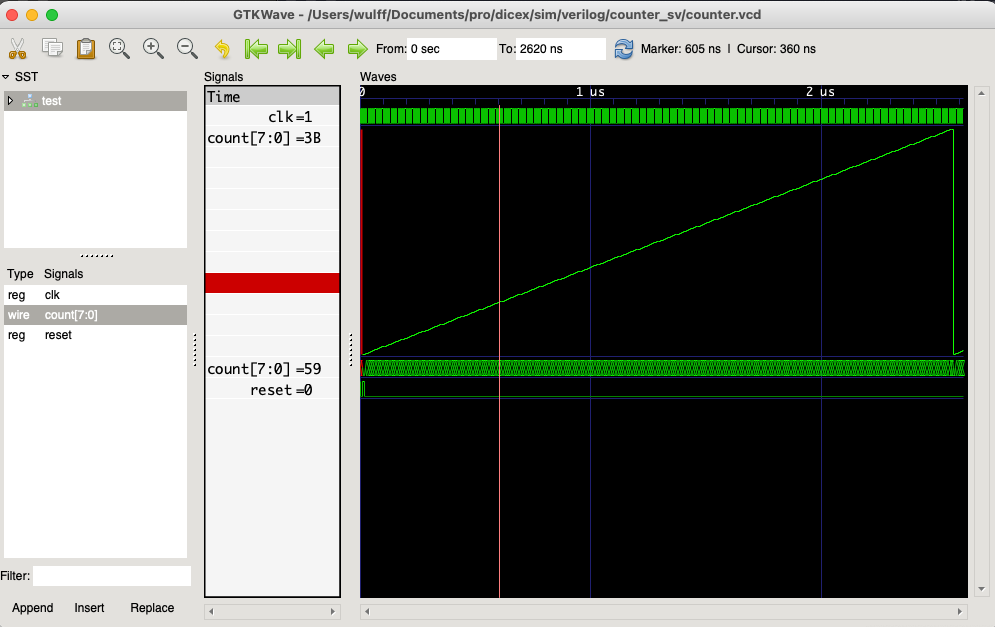
Attack vector

module counter(
               output logic [WIDTH-1:0] out,
               input logic              clk,
               input logic              reset
               );

   parameter WIDTH = 8;

   logic [WIDTH-1:0]                    count;
   always_comb begin
      count = out + 1;
   end

   always_ff @(posedge clk or posedge reset) begin
      if (reset)
        out <= 0;
      else
        out <= count;
   end

endmodule // counter



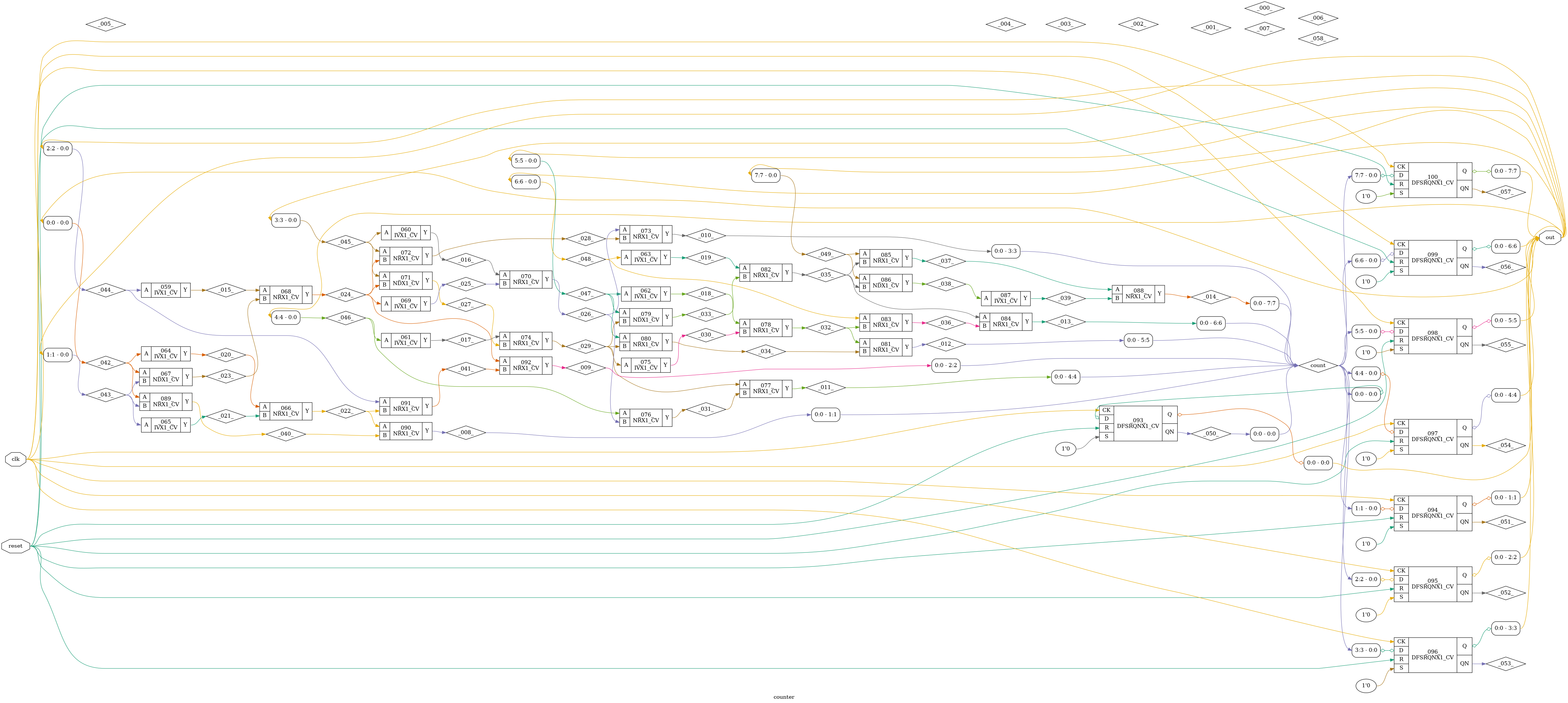
.SUBCKT counter out_7 out_6 out_5 out_4 out_3 out_2 out_1 out_0 clk reset AVDD AVSS
* SPICE netlist generated by Yosys 0_9 (git sha1 1979e0b1, gcc 10_3_0-1ubuntu1~20_10 -fPIC -Os)
X0 out_2 1 AVDD AVSS IVX1_CV
X1 out_3 2 AVDD AVSS IVX1_CV
X2 out_4 3 AVDD AVSS IVX1_CV
X3 out_5 4 AVDD AVSS IVX1_CV
X4 out_6 5 AVDD AVSS IVX1_CV
X5 out_0 6 AVDD AVSS IVX1_CV
X6 out_1 7 AVDD AVSS IVX1_CV
X7 6 7 8 AVDD AVSS NRX1_CV
X8 out_0 out_1 9 AVDD AVSS NDX1_CV
X9 1 9 10 AVDD AVSS NRX1_CV
X10 10 11 AVDD AVSS IVX1_CV
X11 2 11 12 AVDD AVSS NRX1_CV
X12 out_3 10 13 AVDD AVSS NDX1_CV
X13 out_3 10 14 AVDD AVSS NRX1_CV
X14 12 14 15 AVDD AVSS NRX1_CV
X15 3 13 16 AVDD AVSS NRX1_CV
X16 16 17 AVDD AVSS IVX1_CV
X17 out_4 12 18 AVDD AVSS NRX1_CV
X18 16 18 19 AVDD AVSS NRX1_CV
X19 4 17 20 AVDD AVSS NRX1_CV
X20 out_5 16 21 AVDD AVSS NDX1_CV
X21 out_5 16 22 AVDD AVSS NRX1_CV
X22 20 22 23 AVDD AVSS NRX1_CV
X23 5 21 24 AVDD AVSS NRX1_CV
X24 out_6 20 25 AVDD AVSS NRX1_CV
X25 24 25 26 AVDD AVSS NRX1_CV
X26 out_7 24 27 AVDD AVSS NRX1_CV
X27 out_7 24 28 AVDD AVSS NDX1_CV
X28 28 29 AVDD AVSS IVX1_CV
X29 27 29 30 AVDD AVSS NRX1_CV
X30 out_0 out_1 31 AVDD AVSS NRX1_CV
X31 8 31 32 AVDD AVSS NRX1_CV
X32 out_2 8 33 AVDD AVSS NRX1_CV
X33 10 33 34 AVDD AVSS NRX1_CV
X34 35 clk AVSS reset out_0 35 AVDD AVSS DFSRQNX1_CV
X35 32 clk AVSS reset out_1 36 AVDD AVSS DFSRQNX1_CV
X36 34 clk AVSS reset out_2 37 AVDD AVSS DFSRQNX1_CV
X37 15 clk AVSS reset out_3 38 AVDD AVSS DFSRQNX1_CV
X38 19 clk AVSS reset out_4 39 AVDD AVSS DFSRQNX1_CV
X39 23 clk AVSS reset out_5 40 AVDD AVSS DFSRQNX1_CV
X40 26 clk AVSS reset out_6 41 AVDD AVSS DFSRQNX1_CV
X41 30 clk AVSS reset out_7 42 AVDD AVSS DFSRQNX1_CV
V0 count_0 35 DC 0
V1 43 out_2 DC 0
V2 44 out_3 DC 0
V3 count_3 15 DC 0
V4 45 out_4 DC 0
V5 count_4 19 DC 0
V6 46 out_5 DC 0
V7 count_5 23 DC 0
V8 47 out_6 DC 0
V9 count_6 26 DC 0
V10 48 out_7 DC 0
V11 count_7 30 DC 0
V12 49 out_0 DC 0
V13 50 out_1 DC 0
V14 count_1 32 DC 0
V15 count_2 34 DC 0
.ENDS

dicex/sim/verilog/counter_sv/counter_attack_tb.cir

VDDA AVDD_ATTACK 0 dc 0.5 pulse(1.5 0.6 tcd trf trf tapw taper)

  1. PVT \(\Rightarrow\) Process, Voltage, Temperature ↩ ↩2

  2. Opportunity for good programmers ↩