Slides

TFE4152 - Lecture 13

CMOS Logic

Source

Week Book Monday Book Friday
34   Introduction, what are we going to do in this course. Why do you need it? WH 1 , WH 15 Manufacturing of integrated circuits
35 CJM 1.1 pn Junctions CJM 1.2 WH 1.3, 2.1-2.4 Mosfet transistors
36 CJM 1.2 WH 1.3, 2.1-2.4 Mosfet transistors CJM 1.3 - 1.6 Modeling and passive devices
37   Guest Lecture - Sony CJM 3.1, 3.5, 3.6 Current mirrors
38 CJM 3.2, 3.3,3.4 3.7 Amplifiers CJM, CJM 2 WH 1.5 SPICE simulation
39   Verilog   Verilog
40 WH 1.4 WH 2.5 CMOS Logic WH 3 Speed
41 WH 4 Power WH 5 Wires
42 WH 6 Scaling Reliability and Variability WH 8 Gates
43 WH 9 Sequencing WH 10 Datapaths - Adders
44 WH 10 Datapaths - Multipliers, Counters WH 11 Memories
45 WH 12 Packaging WH 14 Test
46   Guest lecture - Nordic Semiconductor    
47 CJM Recap of CJM WH Recap of WH

Goal for today

Analog transistor to digital transistor

Fundamental static logic cells

Other static logic cells

Project Questions

(If time: Sesame Demo)

Analog transistor to digital transistor

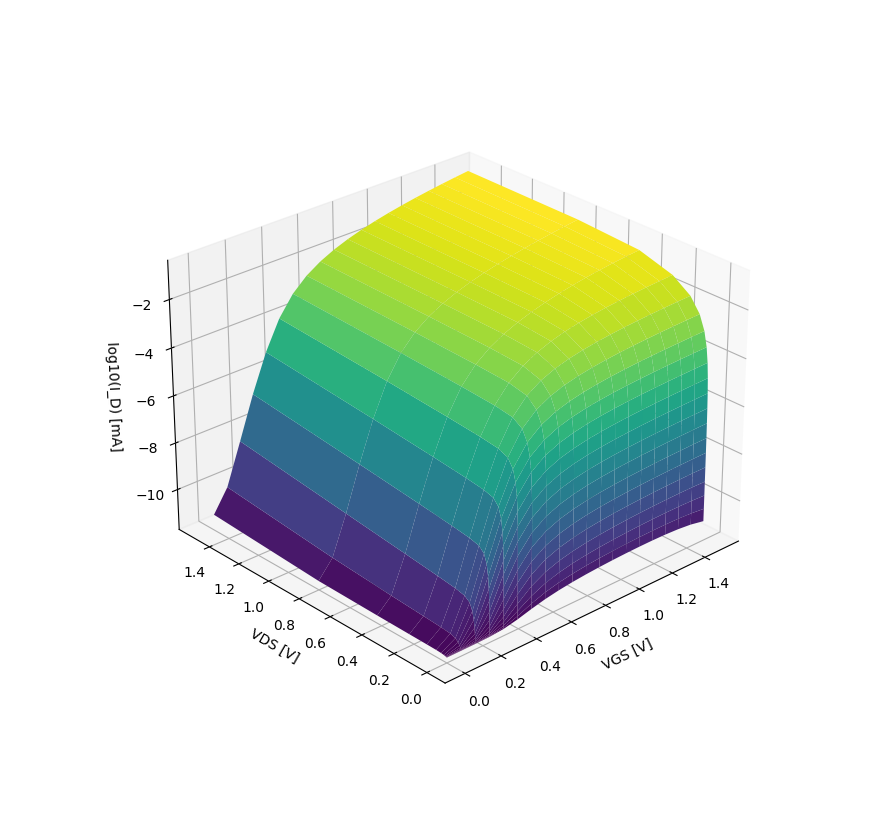
NMOS current (W = 0.4u L=0.15u) as a function of \(V_{GS}\) and \(V_{DS}\)

dicex/lectures/l13/mos.py

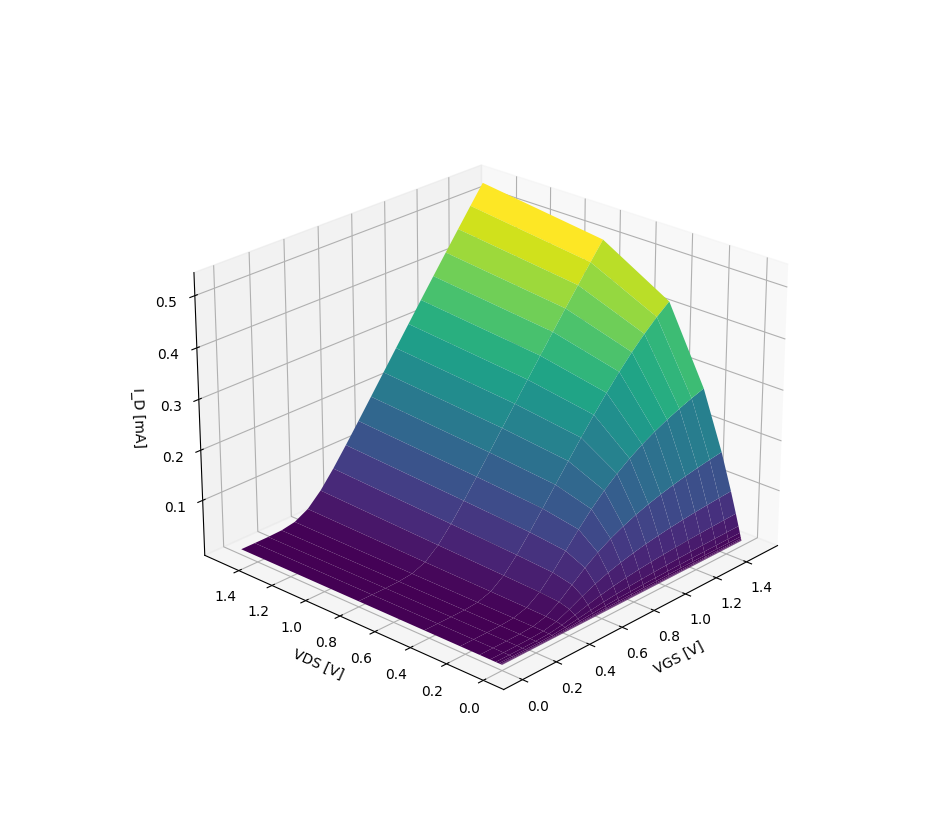
Gate NMOS PMOS
VDD ON OFF
VDD -> VSS X X
VSS -> VDD X X
VSS OFF ON
Gate NMOS PMOS
1 ON OFF
1 -> 0 X X
0 -> 1 X X
0 OFF ON

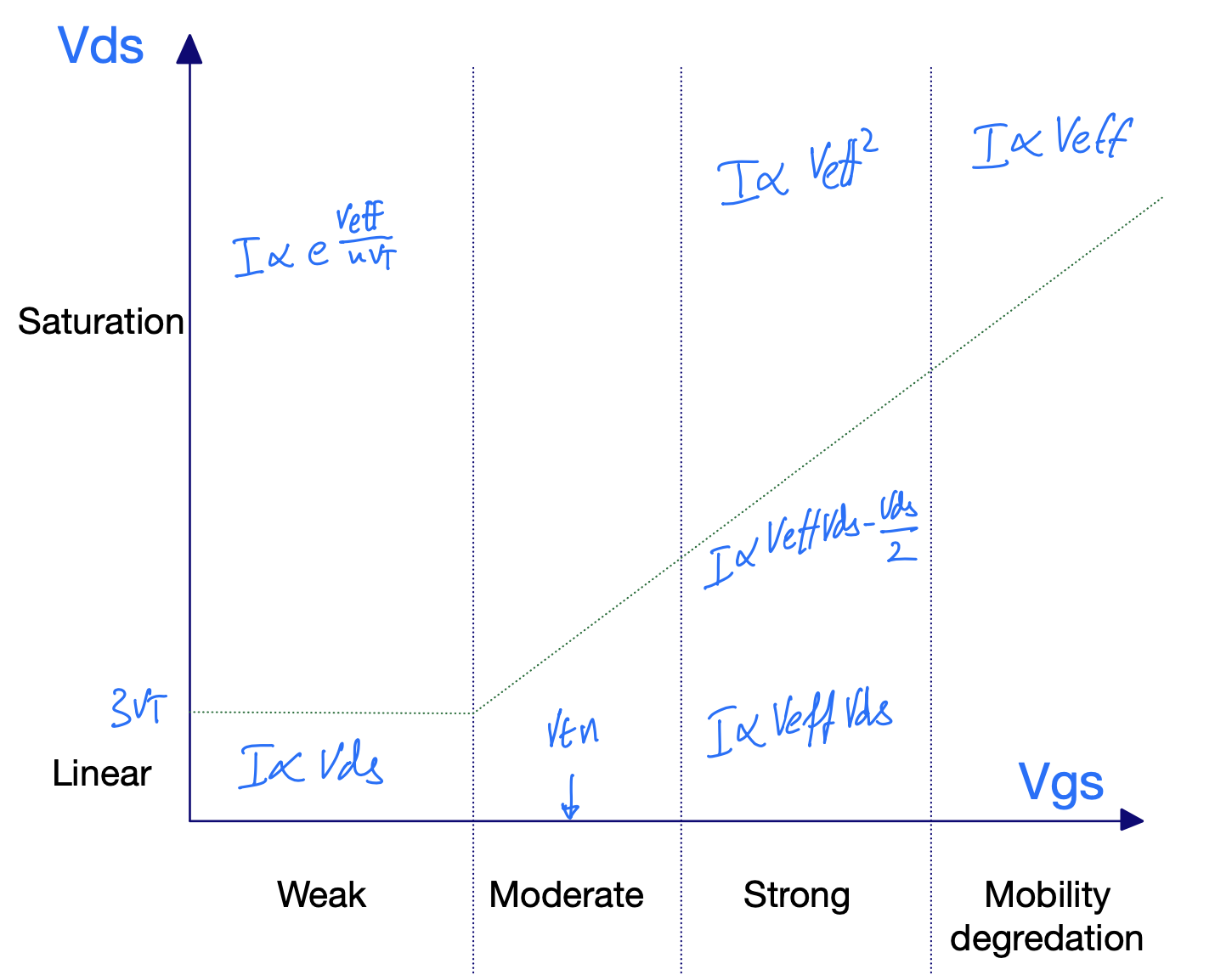
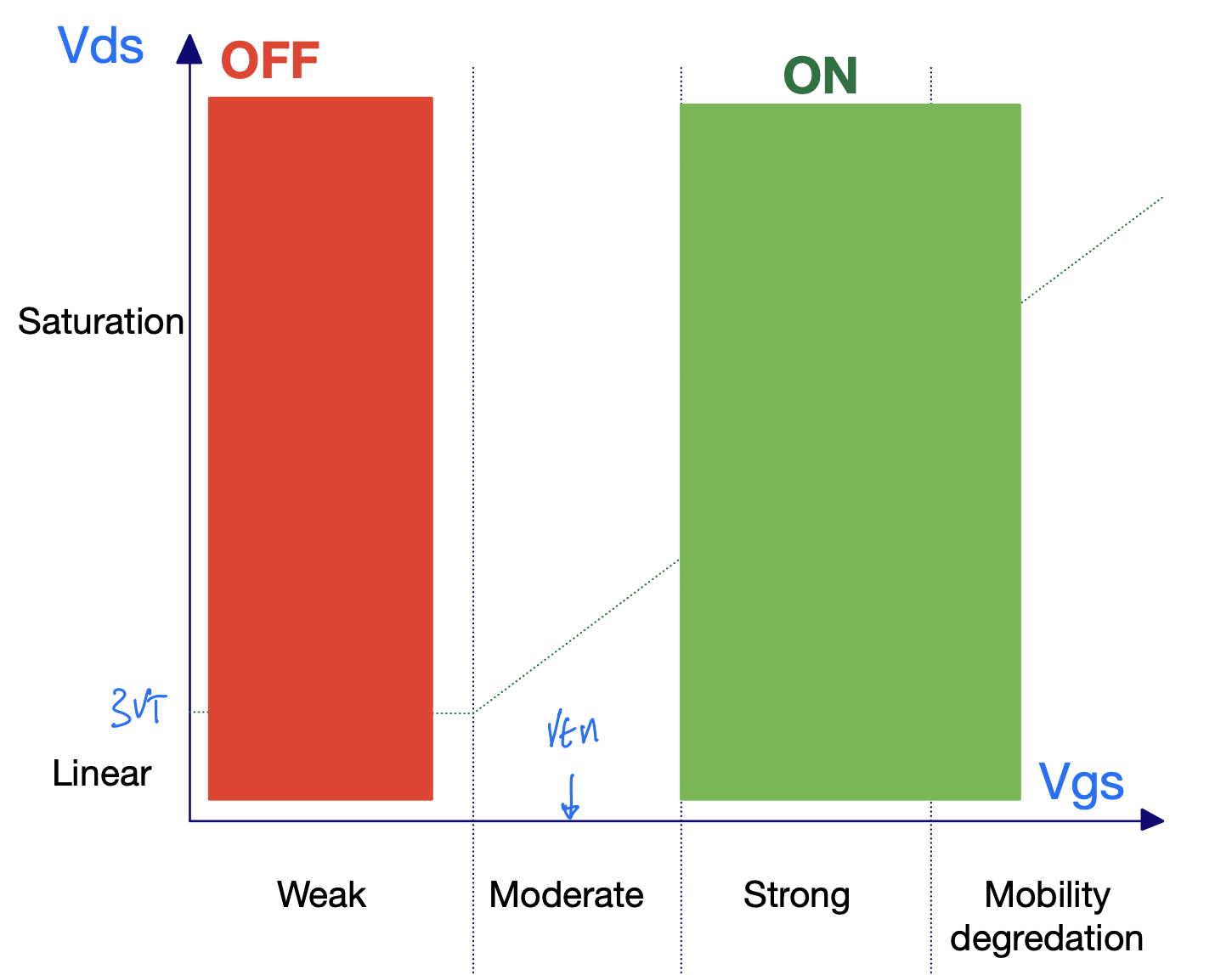
CMOS static logic assumptions

NMOS source is connected to low potential

\(V_{GS} > V_{TH}\) when \(V_G = V_{DD}\)

PMOS source is connected to high potential

\(V_{GS} < V_{TH}\) when \(V_G = 0\)

Don’t break rules unless you know exactly why it will be OK

Logic cells

CMOS static logic is inverting

A Y
1 0
0 1

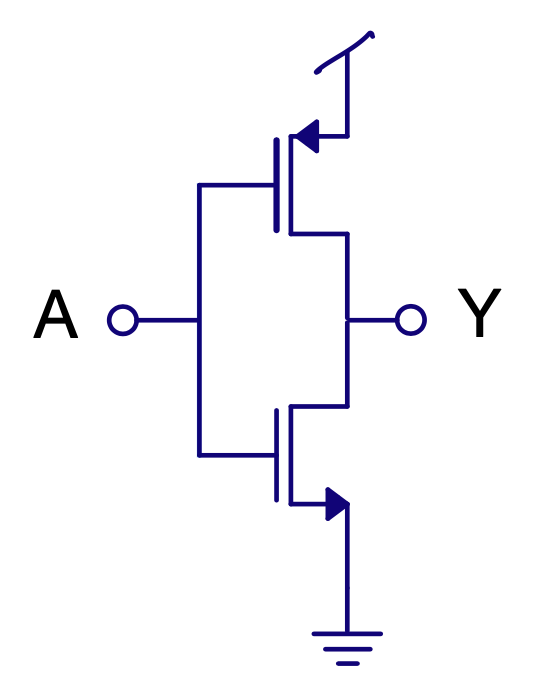
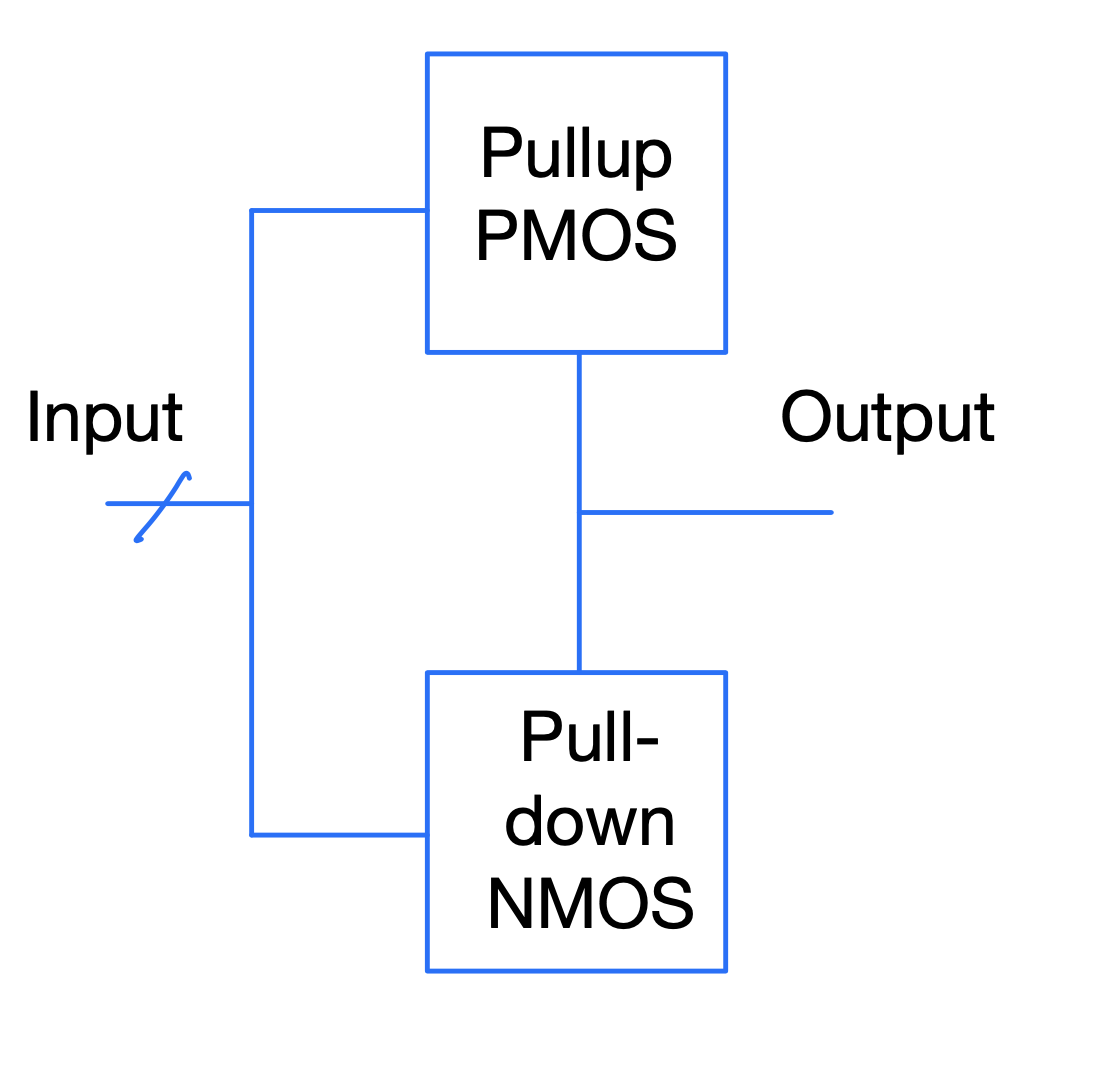
PD = Pull-down PU = Pull-up

logic => [0,1,Z,X];

[.table-separator: #000000, stroke-width(1)] [.table: margin(8)]

Pull-up series

A B Y
0 0 1
0 1 Z
1 0 Z
1 1 Z

Pull-up paralell

A B Y
0 0 1
0 1 1
1 0 1
1 1 Z

[.table-separator: #000000, stroke-width(1)] [.table: margin(8)]

Pull-down series

A B Y
0 0 Z
0 1 Z
1 0 Z
1 1 0

Pull-down paralell

A B Y
0 0 Z
0 1 0
1 0 0
1 1 0

Rules for inverting logic

Pull-up OR \(\Rightarrow\) PMOS in series \(\Rightarrow\) POS AND \(\Rightarrow\) PMOS in paralell \(\Rightarrow\) PAP

Pull-down OR \(\Rightarrow\) NMOS in paralell \(\Rightarrow\) NOP AND \(\Rightarrow\) NMOS in series \(\Rightarrow\) NAS

Memnonic

Crazier the better

POS, PAP, NOP, NAS

A Postraumatic Papaya was walking on the Moon. Nope, it was a NASA astronaut.

image ../ip/moonwalking.jpg removed Moonwalking with Einstein

[.table-separator: #000000, stroke-width(1)] [.table: margin(8)]

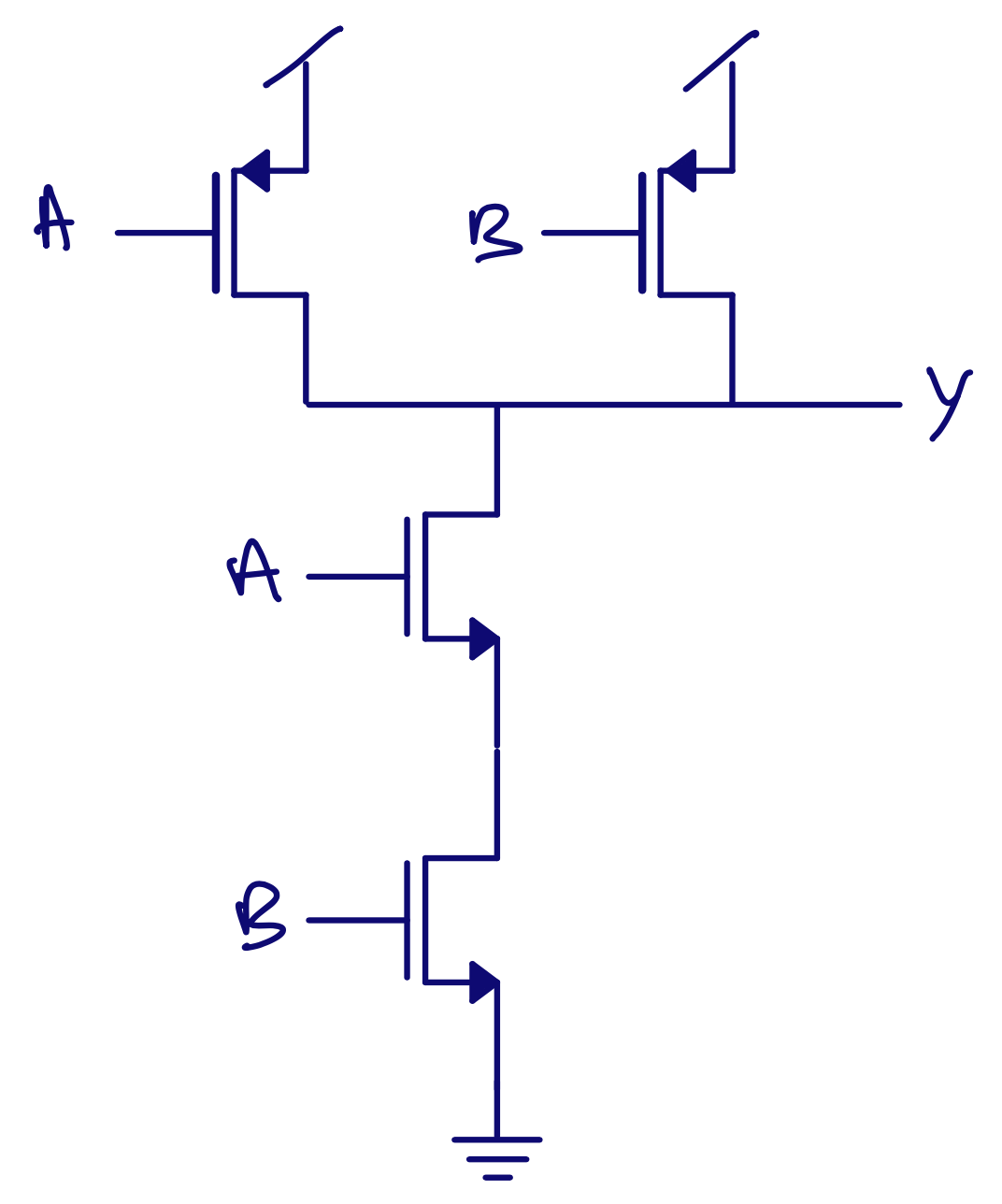
\(\text{Y} = \overline{\text{AB}} = \text{NOT ( A AND B)}\)

AND PU \(\Rightarrow\) PMOS in paralell PD \(\Rightarrow\) NMOS in series

A Postraumatic Papaya was walking on the Moon. Nope, it was a NASA astronaut.

A B NOT(A AND B)
0 0 1
0 1 1
1 0 1
1 1 0

[.table-separator: #000000, stroke-width(1)] [.table: margin(8)]

\(\text{Y} = \overline{\text{A + B}} = \text{NOT ( A OR B)}\)

OR PU \(\Rightarrow\) PMOS in series PD \(\Rightarrow\) NMOS in paralell

A Postraumatic Papaya was walking on the Moon. Nope, it was a NASA astronaut.

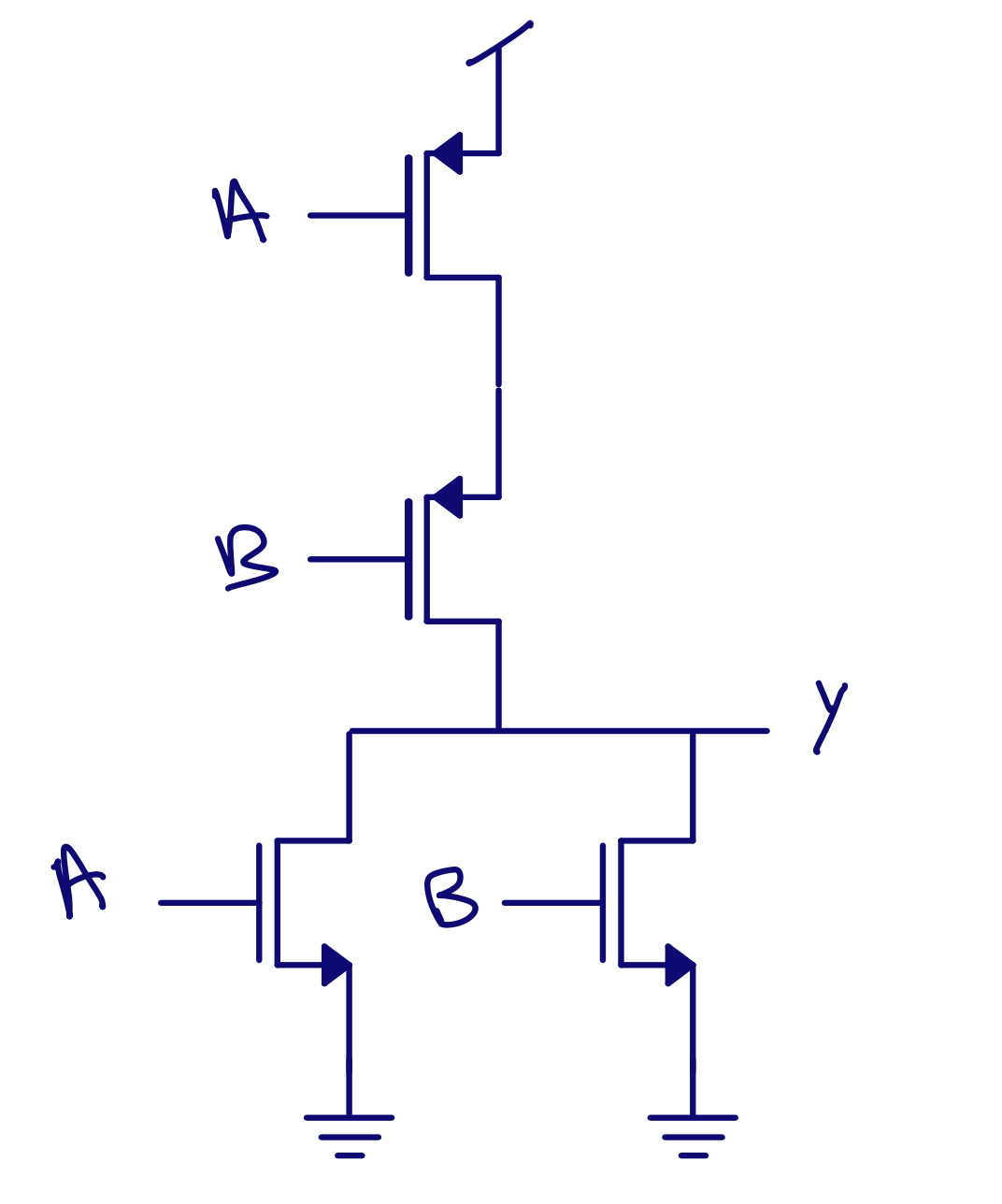
A B NOT(A OR B)
0 0 1
0 1 0
1 0 0
1 1 0

\(SR\)-Latch

Use boolean expressions to figure out how gates work.

Remember De-Morgan

\(\overline{AB} = \overline{A}+ \overline{B}\) \(\overline{A+B} = \overline{A} \cdot \overline{B}\)

\[Q = \overline{R \overline{Q}} = \overline{R} + \overline{\overline{Q}} = \overline{R} + Q\] \[\overline{Q} = \overline{S Q} = \overline{S} + \overline{Q} = \overline{S} + \overline{Q}\]

\(SR\)-Latch

\(Q = \overline{R} + Q\), \(\overline{Q} =\overline{S} + \overline{Q}\)

S R Q ~Q
0 0 X X
0 1 0 1
1 0 1 0
1 1 Q ~Q

D-Latch (16 transistors)

C D Q ~Q
0 X Q ~Q
1 0 0 1
1 1 1 0

Digital can be synthesized in conductive peanut butter Barrie Gilbert?

Other logic cells

What about \(\text{Y} = \text{AB}\) and \(\text{Y} = \text{A} + \text{B}\)?

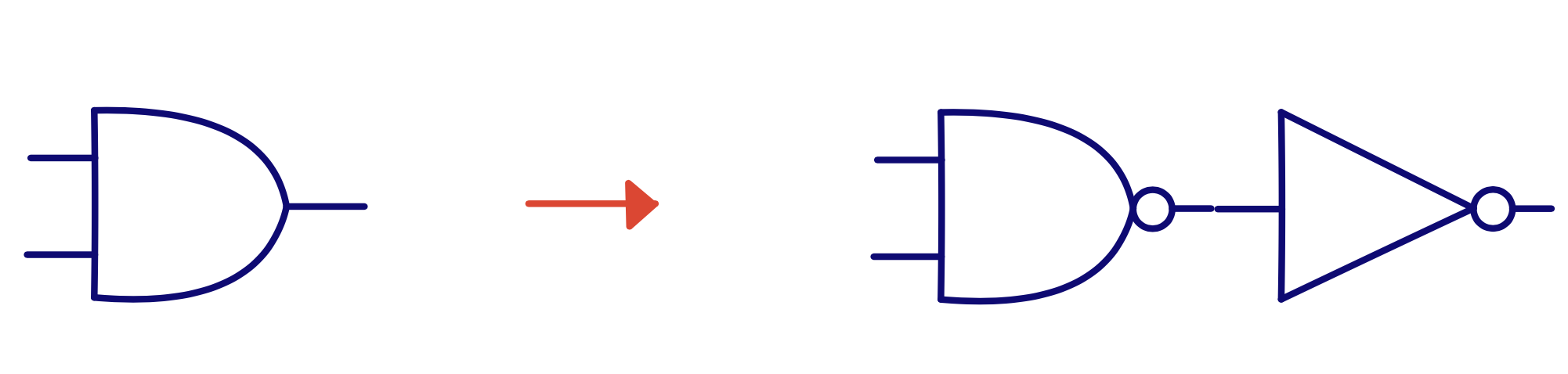
\(\text{Y} = \text{AB} = \overline{\overline{\text{AB}}}\)

Y = A AND B = NOT( NOT( A AND B ) )

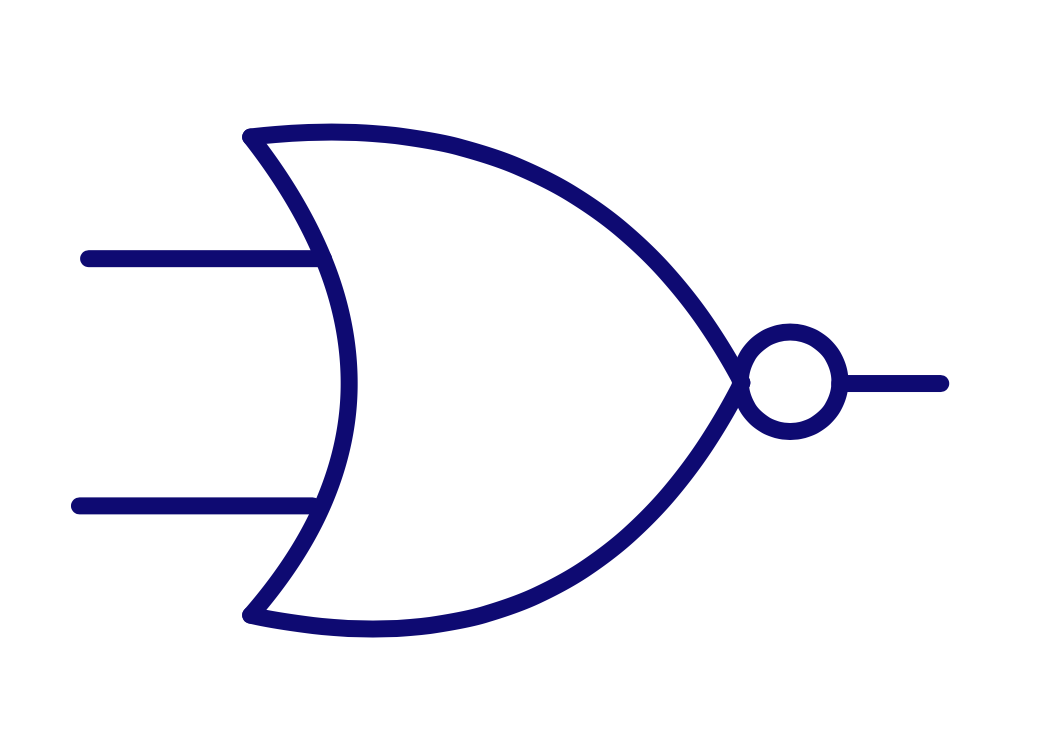
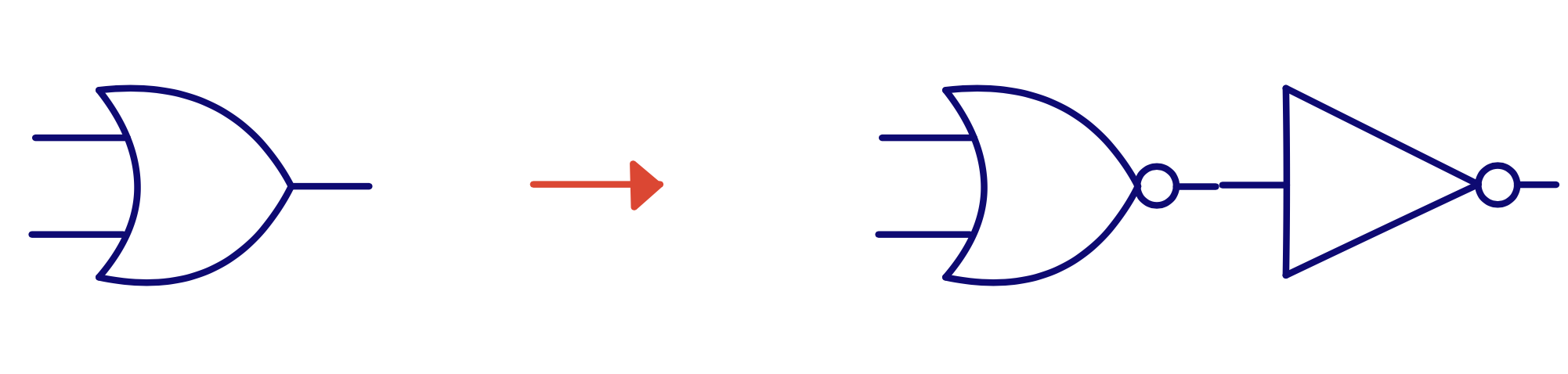
\(\text{Y} = \text{A+B} = \overline{\overline{\text{A+B}}}\)

Y = A OR B = NOT( NOT( A OR B ) )

AOI22: and or invert

Y = NOT( A AND B OR C AND D)

\[\text{Y} = \overline{\text{AB} + \text{CD}}\]

A Postraumatic Papaya was walking on the Moon. Nope, it was a NASA astronaut.

[.table-separator: #000000, stroke-width(1)] [.table: margin(8)]

Tristate inverter

E A Y
0 0 Z
0 1 Z
1 0 1
1 1 0

[.table-separator: #000000, stroke-width(1)] [.table: margin(8)]

Mux

S Y
0 NOT(P1)
0 NOT(P1)
1 NOT(P0)
1 NOT(P0)

D-Latch (12 transistors)

D-Flip Flop (< 26 transistors)

There are other types of logic

  • True single phase clock (TSPC) logic
  • Pass transistor logic
  • Transmission gate logic
  • Differential logic
  • Dynamic logic

Consider other types of logic “rule breaking”, so you should know why you need it.

Dynamic logic => A Compiled 9-bit 20-MS/s 3.5-fJ/conv.step SAR ADC in 28-nm FDSOI for Bluetooth Low Energy Receivers

Zen of electronics design 1

Beautiful is better than ugly.

Explicit is better than implicit.

Simple is better than complex.

Complex is better than complicated.

Readability counts.

Special cases aren’t special enough to break the rules.

Although practicality beats purity.

In the face of ambiguity, refuse the temptation to guess.

Now is better than never.

Although never is often better than right now.

If the implementation is hard to explain, it’s a bad idea.

If the implementation is easy to explain, it may be a good idea.

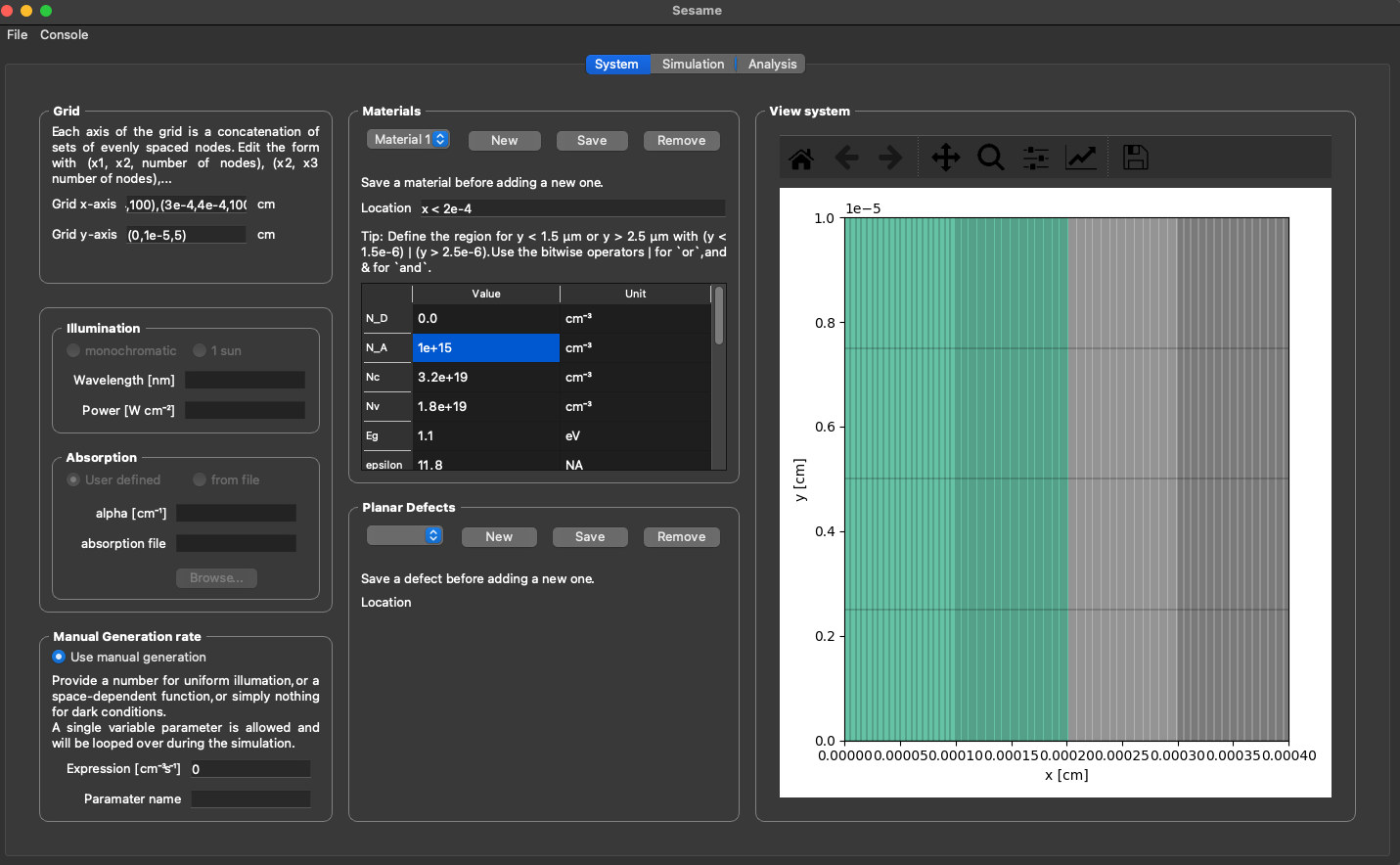
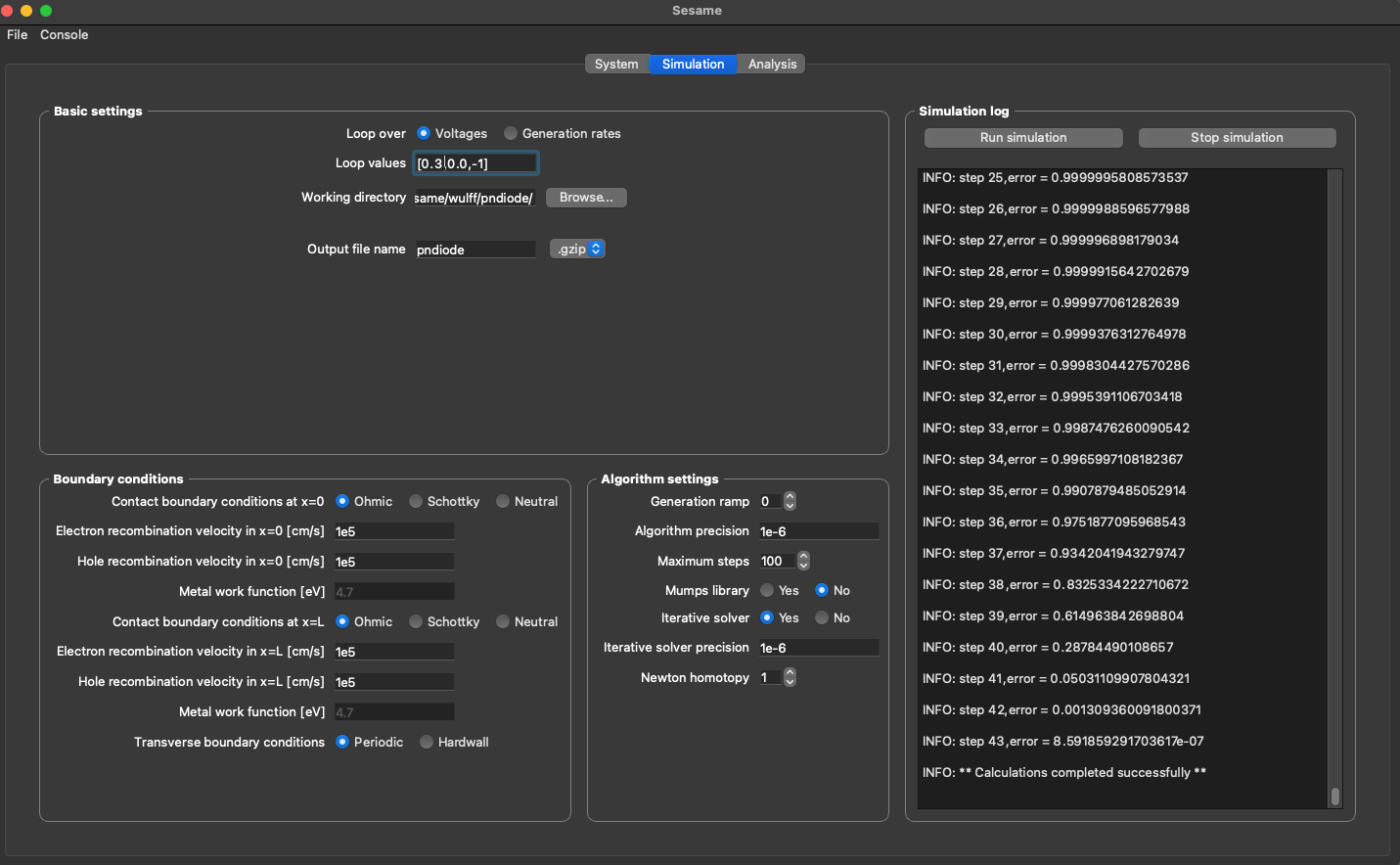
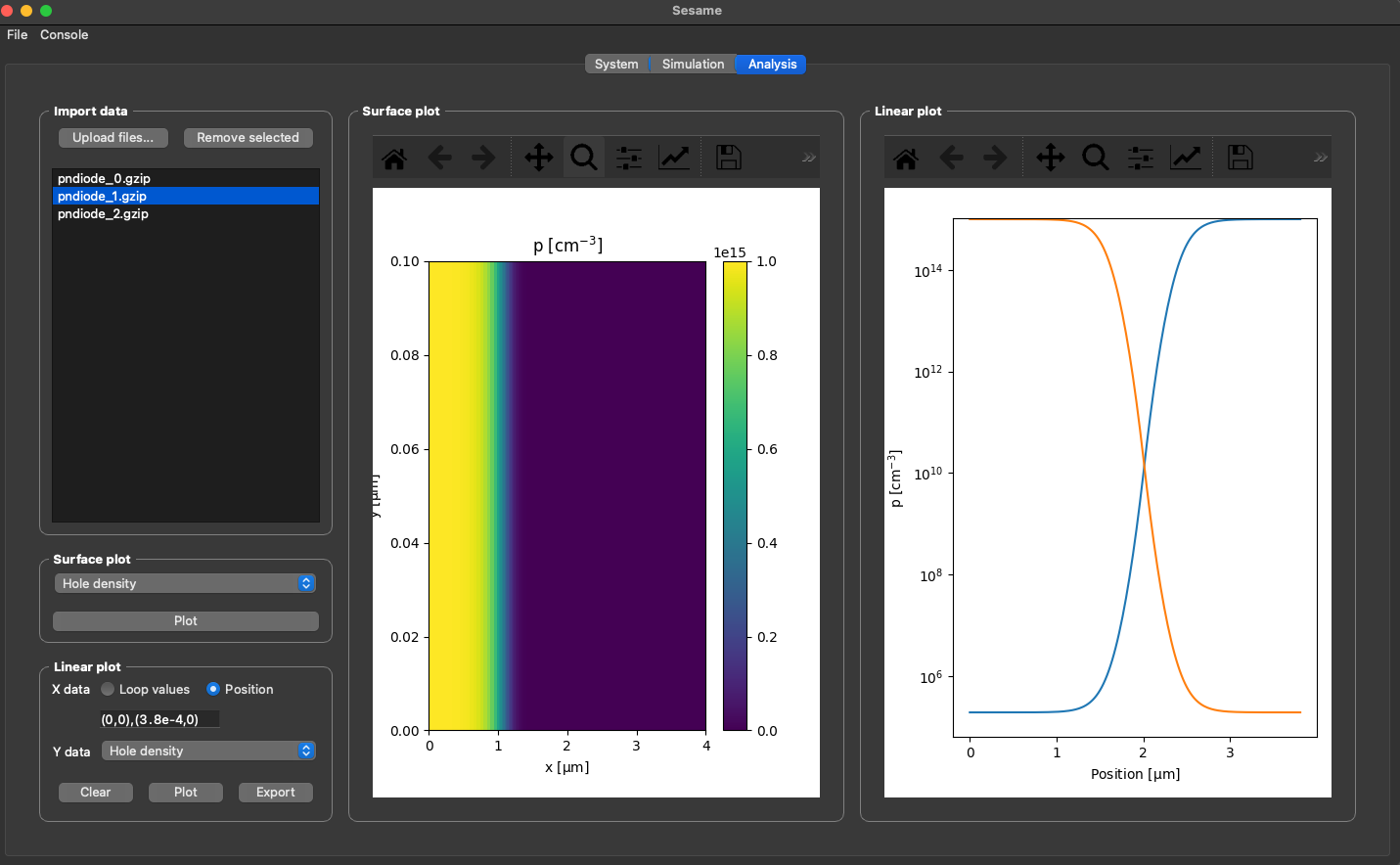
Sesame

Sesame is a Python3 package for solving the drift diffusion Poisson equations for multi-dimensional systems using finite differences.

Install instructions

Semiconductor current-flow equations (diffusion and degeneracy), R.Stratton, IEEE Transactions on Electron Devices https://ieeexplore.ieee.org/document/1477063

  1. Zen of Python ↩