If you find an error in what I’ve made, then fork, fix lectures/l04_mac.md, commit, push and create a pull request. That way, we use the global brain power most efficiently, and avoid multiple humans spending time on discovering the same error.

\[a_{l+1} = \sigma(W_l a_l + b_l)\]

A NN consists of addition, multiplication, and a non-linear function

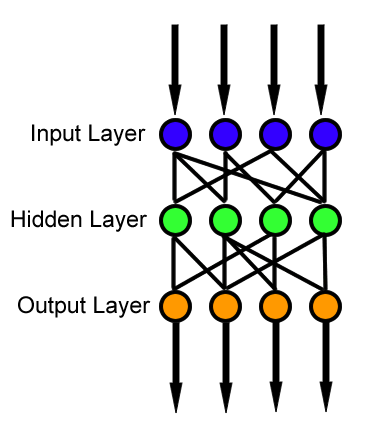
\[\mathbf{y} = \sigma\left(\begin{bmatrix} w_{11} & w_{12} & \ldots & w_{1n} \\ w_{21} & w_{22} & \ldots & w_{2n} \\ \vdots & \vdots & \ddots & \vdots \\ w_{m1} & w_{m2} & \ldots & w_{mn} \end{bmatrix} \begin{bmatrix} x_1 \\ x_2 \\ \vdots \\ x_n \end{bmatrix} + \begin{bmatrix} b_1 \\ b_2 \\ \vdots \\ b_m \end{bmatrix}\right)\] \[{\mathrm{ OA}}_{(x,y,k)} = f \left ({\sum _{i=0}^{R-1} \sum _{j=0}^{S-1} \sum _{c=0}^{C-1} {\mathrm{ IA}}_{(x+i,y+j,c)} \times W_{(i,j,c,k)} }\right)\]

Assume N neurons

N multiplications per neuron
N + 1 additions per neuron
1 sigmoid per neuron

For efficient inference, additions and multiplications should be low power!

Kirchoff’s voltage law

The directed sum of the potential differences around any closed loop is zero

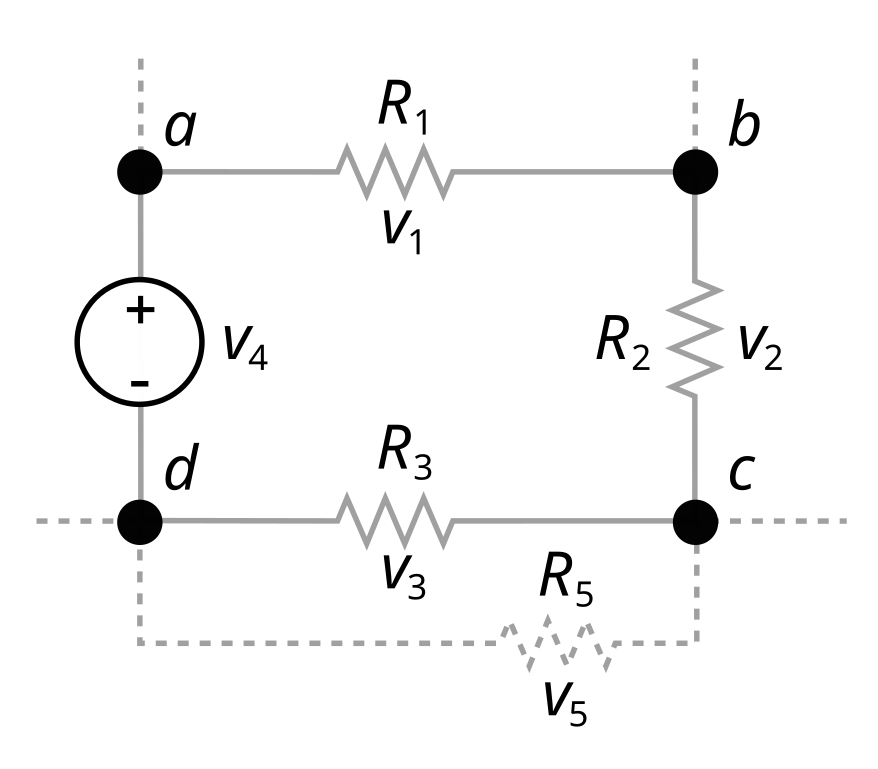
\(V_1 + V_2 + V_3 + V_4 = 0\)

Kirchoff’s current law

The algebraic sum of currents in a network of conductors meeting at a point is zero

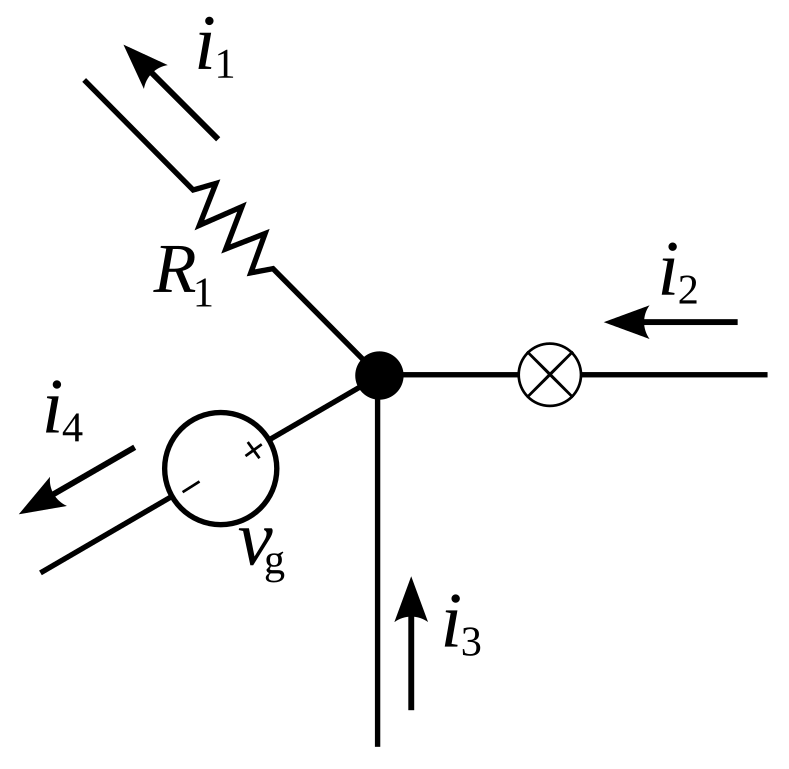
\(i_1 + i_2 + i_3 + i_4 = 0\)

Charge concervation

See Charge concervation on Wikipedia

\[Q_4 = Q_1 + Q_2 + Q_3\] \[V_4 = \frac{ C_1 V_1 + C_2 V_2 + C_3 V_3}{C_1 + C_2 + C_3}\]

Multiplication

Digital capacitance

\[V_4 = \frac{ C_1 V_1 + C_2 V_2 + C_3 V_3}{C_1 + C_2 + C_3}\] \[V_O = \frac{C_1}{C_{TOT}} V_1 + \dots + \frac{C_N}{C_{TOT}} V_N\]

Make capacitors digitally controlled, then

\[w_1 = \frac{C_1}{C_{TOT}}\]

_{Might have a slight problem with variable gain as a function of total capacitance}

Mixing

\[I_{M1} = G_{m} V_{GS}\] \[I_o = I_{M1} t_{input}\]

Translinear principle

MOSFET in sub-threshold

\[I = I_{D0} \frac{W}{L} e^{(V_{GS} - V_{th})/n U_{T}}\text{ ,} U_T = \frac{k T}{q}\] \[I = \ell e^{V_{GS}/n U_{T}}\text{ , } \ell = I_{D0}\frac{W}{L} e^{-V_{th}/n U_{T}}\] \[V_{GS} = n U_{T} \ln\left(\frac{I}{\ell}\right)\]

\[V_1 + V_2 = V_3 + V_4\] \[n U_{T}\left[\ln\left(\frac{I_1}{\ell_1}\right) + \ln\left(\frac{I_2}{\ell_2}\right)\right] = n U_{T}\left[\ln\left(\frac{I_3}{\ell_3}\right) + \ln\left(\frac{I_4}{\ell_4}\right)\right]\] \[\ln\left(\frac{I_1 I_2}{\ell_1 \ell_2}\right) = \ln\left(\frac{I_3 I_4}{\ell_3 \ell_4}\right)\] \[\frac{I_1 I_2}{\ell_1 \ell_2}= \frac{I_3 I_4}{\ell_3 \ell_4}\] \[I_1 I_2 = I_3 I_4\text{ , if } \ell_1 \ell_2= \ell_3 \ell_4\] \[I_1 I_2 = I_3 I_4\] \[I_1 = I_a\text{ ,}I_2 = I_b + i_b\text{ ,}I_3 = I_b\text{ ,}I_4 = I_a + i_a\] \[I_a (I_b + i_b) = I_b (I_a + i_a)\] \[I_a I_b + I_a i_b = I_b I_a + I_b i_a\] \[i_b = \frac{I_b}{I_a} i_a\] \[\ell_1 \ell_2= \ell_3 \ell_4\] \[\ell_1 = I_{D0}\frac{W}{L} e^{-V_{th}/n U_{T}}\] \[\ell_2 = I_{D0}\frac{W}{L} e^{-(V_{th} \pm \sigma_{th})/n U_{T}} = \ell_1 e^{\pm \sigma_{th}/n U_{T}}\] \[\sigma_{th} = \frac{a_{vt}}{\sqrt{W L}}\] \[\frac{\ell_2}{\ell_1} = e^{\pm \frac{a_{vt}}{\sqrt{W L}}/n U_{T}}\]

Demo

JNW_SV_SKY130A

Want to learn more?

An Always-On 3.8 u J/86 % CIFAR-10 Mixed-Signal Binary CNN Processor With All Memory on Chip in 28-nm CMOS

CAP-RAM: A Charge-Domain In-Memory Computing 6T-SRAM for Accurate and Precision-Programmable CNN Inference

ARCHON: A 332.7TOPS/W 5b Variation-Tolerant Analog CNN Processor Featuring Analog Neuronal Computation Unit and Analog Memory

IMPACT: A 1-to-4b 813-TOPS/W 22-nm FD-SOI Compute-in-Memory CNN Accelerator Featuring a 4.2-POPS/W 146-TOPS/mm2 CIM-SRAM With Multi-Bit Analog Batch-Normalization