Errare humanum est, sed perseverare diabolicum

I enjoy learning, and right now, I’m trying to understand a bit more of quantum mechanics. The source I’m using is the Feynman Lectures of Physics, however, I like reading physical books, and not online, on my mac or my iPad.

I was reading a section on “The size of the atom”, which, in my physical book, is section 2-6 in volume III, and I ran into trouble. Let me try to explain the story.

“The size of the atom” retold

I’ll paraphrase Feynman’s story. We know it’s impossible to determine both position and momentum of an electron exactly, also known as the Heisenberg uncertainty principle

\[\Delta x \Delta p \approx h\]

, where $\Delta x$ is the position uncertainty, $\Delta p$ is the momentum uncertainty, and $h$ is Planck constant.

Assume a Hydrogen atom, with one proton and one electron. We assume the distance from nucleus to electron is $a \approx \Delta x$. The momentum is roughly

\[p \approx \frac{h}{a}\]

Feynman has a beautiful derivation. The kinetic energy is approximately

\[E_k = \frac{1}{2} m v^2 = \frac{p^2}{2 m} = \frac{h^2}{2 m a^2}\]

, where $m$ is the rest mass of the electron, and $p = mv$.

The electric potential energy between the proton and electron is

\[E_p = -\frac{q^2}{4 \pi \epsilon_0 a}\]

, where $\epsilon_0$ is the vacuum permittivity, and $q$ the elementary charge. The negative energy just means the electron and proton attract eachother.

The total energy is

\[E = E_k + E_p = \frac{h^2}{2 m a^2} -\frac{q^2}{4 \pi \epsilon_0 a}\]

We know that the atom will settle at some $a$ and an energy minimum. We can estimate the energy minimum distance $a_0$ by taking the derivative of the energy as a function of distance and set the derivative to zero.

\[\frac{dE}{da} = -\frac{h^2}{m a^3} + \frac{q^2}{4 \pi \epsilon_0 a^2 } = 0\]

Solved for $a$ we get

\[a_0 = \frac{h^2 4 \pi \epsilon_0}{ m q^2}\]

In the book, $a_0$ is boldy stated as

\[a_0 = 0.528 \times 10^{-10}\text{ meter }\]

The trouble

I wanted to see if I could get the same number for $a$, so I set about inserting for the constants1. Instead of using the numbers I found the current definition of vacuum permittivity.

\[\epsilon_0 = \frac{1}{\mu_0 c^2}\]

, where $c$ is the speed of light, and $\mu_0$ is the vacuum permeability, which, in SI units, is now

\[\mu_0 = \frac{2 \alpha}{q^2}\frac{h}{c}\]

, where $\alpha$ is the fine structure constant.

As a result

\[\epsilon_0 = \frac{q^2 c}{2 \alpha h c^2} = \frac{q^2 }{2 \alpha }\frac{1}{hc}\]

I inserted into the equation for $a_0$, and most of the constants canceled

\[a_0 = \left[4\pi h^2 \frac{1}{hc}\frac{q^2}{2 \alpha} \right]/m q^2 = \frac{2 \pi }{\alpha }\frac{h}{mc}\]

When computed $a_0 = 2.089\times 10^{-9}\text{ meter }$

Crap, not the same as Feynman!

Double checking

Of course, initially, I thought I must have done something wrong with the maths, so I did the algebra multiple times, but I could not find anything wrong.

Not trusting myself, I did a dimensional analysis.

  • $h$ is Js
  • $m$ is kg
  • $c$ is m/s
  • $\alpha$ is dimensionless
  • J = kg m$^2$/s$^2$

I know that the unit for $a$ is meters, so with the equation for $a_0$

\[\text{m} = \frac{\text{ kg m}^2/\text{s}^2 \times \text{s}}{\text{kg }\text{m/s}} = \text{m}\]

Hmmpf, so the unit is correct. What could I have done wrong!

Stumble around

When I can’t figure out what’s wrong I stumble around, poke and prod, or just try things.

Maybe I go the $2\pi$ wrong? Time for python coding

from scipy import constants
pi = constants.pi
h = constants.physical_constants["Planck constant"][0]
alpha = constants.physical_constants["fine-structure constant"][0]
c = constants.physical_constants["speed of light in vacuum"][0]
me = constants.physical_constants["electron mass"][0]

#- Feynman's number
a0f = 0.528e-10
print("a0f = %g"%a0f)

#- Calculation of a_0 from constants
a0 = (2*pi*1/alpha * h/c/me)
print("a0 = %g"%a0)

#- Remove the 2pi and check versus Feynmans number
a1 = (1/alpha * h/c/me)
print("a1 = %g"%a1)
print("a1/a0f = %g"%(a1/a0f))

Output:

a0f = 5.28e-11
a0 = 2.08911e-09
a1 = 3.32492e-10
a1/a0f = 6.29719

Eureka! There is a $(1/2\pi)^2$ factor wrong in my $a_0$!

Assuming the number from Feynman was correct, the equation should have been

\[a_0 = \frac{1}{ 2 \pi \alpha}\frac{h}{m c}\]

The realization

I was certain had not done the maths wrong, there was no way I could get right equation from where I started.

The starting point from the book was

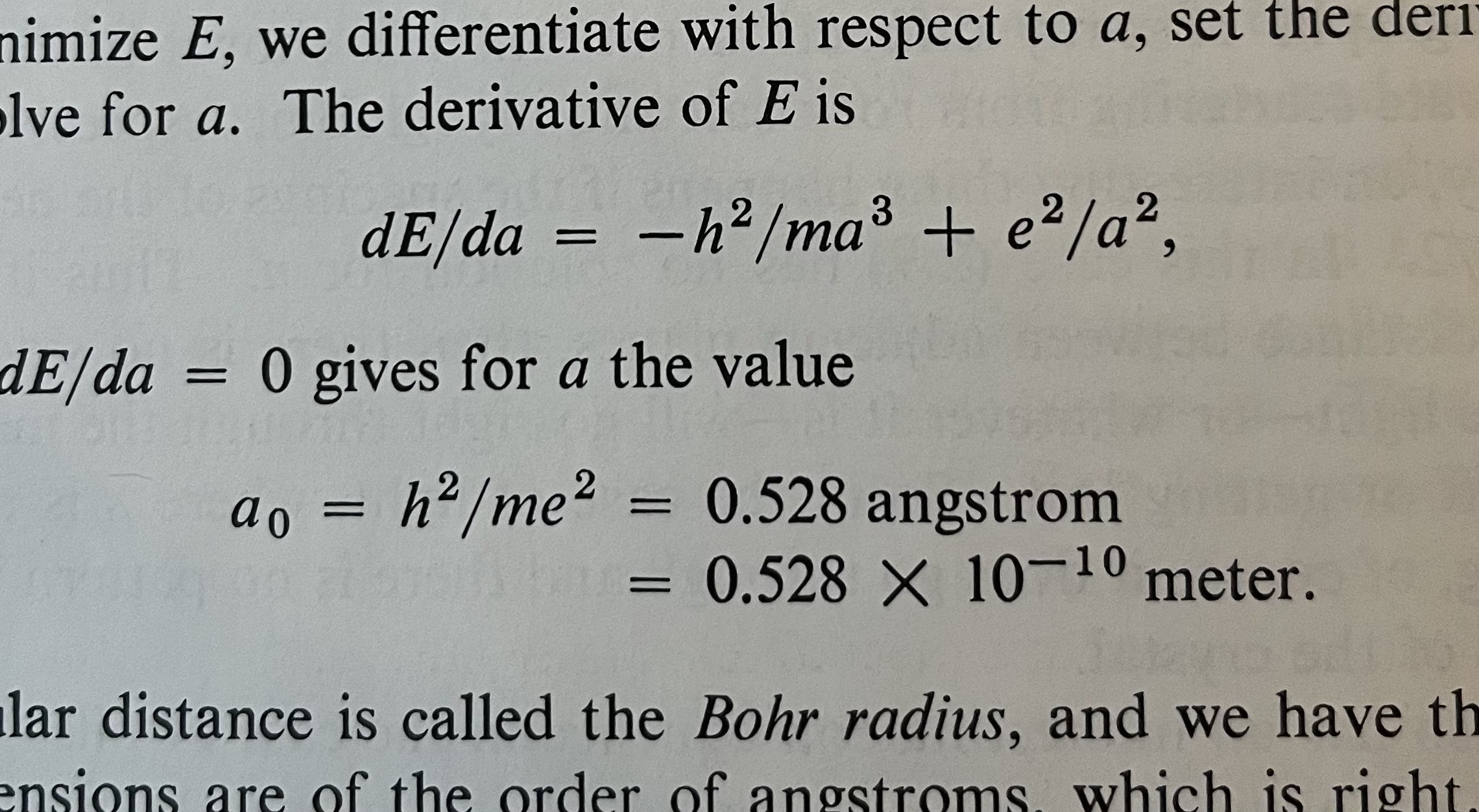
, where $e^2 = q^2/4\pi\epsilon_0$, as such

\[a = \frac{h^2 4 \pi \epsilon_0}{ m q^2}\]

Maybe there was a mistake in the book? If there was a typo, and it should have been

\[a = \frac{\hbar^2 4 \pi \epsilon_0}{ m q^2}\]

, where $\hbar = h/2\pi$, then the result would be correct

\[a_0 = \left[\frac{h^2}{4\pi^2} 4\pi \frac{q^2}{2 \alpha h c} \right]/m q^2 = \frac{1}{ 2 \pi \alpha}\frac{h}{m c}\]

and the world would make sense again. But how could I be certain?

The confirmation

In “The size of the atom”, which is the online version of the lectures, the $h$ is corrected to $\hbar$. I did not do the maths wrong, my physical physics book was wrong (or inaccurate).

I’m not going to blame Feynman. Actually, I’m not going to blame anyone. The book is written by humans, and humans will always make brain farts which lead to errors, that’s just the nature of who we are.

You can’t trust human created information source 100 %. You must have some trust in your own ability. If you check, and check, and check, and can’t find what you did wrong, maybe the error is in the source?

Warning

You are also human, even though you’ve checked $\infty$ number of times, there is still a finite, non-zero, probability that the error is something you did. Don’t be arrogant and always assume the error is caused by others.

You can have an hypothesis that the error is caused by others, but you need to find supporting evidence.

And, since we can only prove an hypothesis false, not true, we can never be 100 % certain what is true, but we can get as close to truth as we want.

On the flip side, since we can prove an hypothesis is false, we can be 100 % certain of what is wrong.

Sidenote

The fact that I will make errors in what I create, and the fact that others might find the errors, is a huge motivation for me to always have anything I create open source on github.

If you find an error in what I’ve made, then fork, fix, commit, push and create a pull request. That way, we use the global brain power most efficiently, and avoid multiple humans spending time on discovering the same error.

  1. I expected that the calculation would be quick, maybe a minute. In reality it took me 4 hours to be satisfied (including this write-up) ↩